题目内容
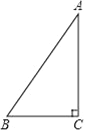
【题目】如图,在△ABC 中,∠C=90°
(1)利用尺规作∠B 的角平分线交AC于D,以BD为直径作⊙O交AB于E(保留作图痕迹,不写作法);
(2)综合应用:在(1)的条件下,连接DE
①求证:CD=DE;
②若sinA=![]() ,AC=6,求AD.
,AC=6,求AD.
【答案】(1)作图见解析;(2)①证明见解析;②AD=![]() .
.
【解析】试题分析:(1)利用角平分线的作法得出∠B的角平分线BD,根据线段垂直平分线的作法作出线段BD的垂直平分线,交BD于点O,以O为圆心,以OB长为半径作圆即可;(2)根据直径所对的圆周角为直角可得∠BED=90°,再由角平分线的性质可得CD=DE;在Rt△ADE中,sinA=![]() =
=![]() ,设DC=DE=3x,AD=5x,根据AC=AD+DC列出方程求得x的值,即可求得AD的长.
,设DC=DE=3x,AD=5x,根据AC=AD+DC列出方程求得x的值,即可求得AD的长.
试题解析:
(1)

(2)∵BD为![]() O的直径
O的直径
∴∠BED=90°,又∵∠C=90°
∴DE⊥AB,DC⊥BC
又∵BD平分∠ABC
∴DE=DC
(3)
在Rt△ADE中,sinA=![]()
∵sinA=![]()
∴![]() =
=![]()
设DC=DE=3![]() ,AD=5
,AD=5![]()
∵AC=AD+DC
∴3![]() +5
+5![]() =6
=6
![]() =
=![]()
AD=5![]() =5×
=5×![]() =
=![]()

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目