题目内容
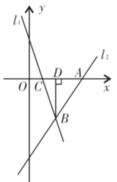
【题目】在平面直角坐标系中，
，
点为
轴上一动点，
.
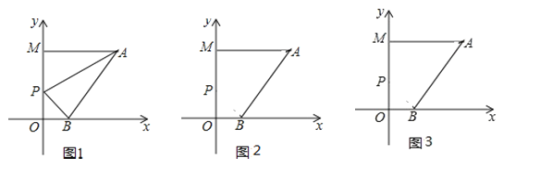
（1）求点
的坐标；
（2）不论点运动到直线
上的任何位置（不包括点
），
三者之间是否都存在某种固定的数量关系，如果有，请利用所学知识找出并证明，如果没有，请说明理由.
【答案】（1）
（2）见解析
【解析】
（1）根据平方、绝对值、二次根式的非负性即可求出a,b,c的值，即可得到坐标；
（2）分三种情况，分别画出图形根据平行线的性质和三角形外角的性质求解即可.
（1）∵
.
∴b-2=0,a-6=0,c-6=0,
∴b=2,a=6,c=6,
∴
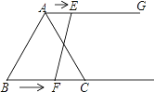
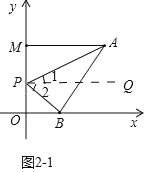
（2）①如图2-1中，点P在线段OM上，结论：∠APB=∠PAM+∠PBO，
理由：作PQ∥AM,则PQ∥AM∥OB
∴∠1=∠PAM，∠2=∠PBO，
∵∠APB=∠1+∠2
∴∠APB=∠PAM+∠PBO
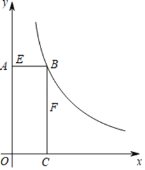
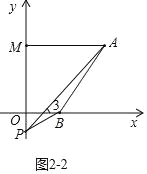
②如图2-2所示，当P在MO延长线上时，结论
理由如下：∵AM∥OB，
∴∠3=
∵∠3=
∴
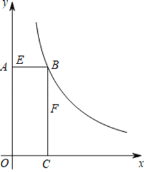
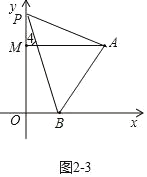
③如图2-3所示，当P在OM延长线上时，结论：
理由如下：∵AM∥OB，
∴∠4=
∵∠4=
∴
练习册系列答案
相关题目
