题目内容
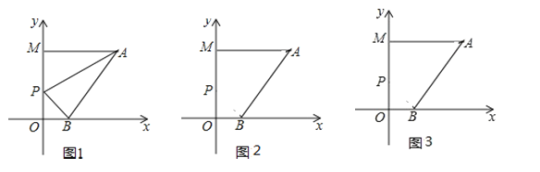
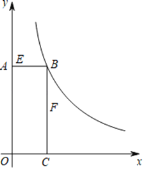
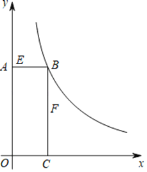
【题目】如图,矩形AOCB的顶点B在反比例函数,x>0)的图像上,且AB=3,BC=8.若动点E从A开始沿AB向B以每秒1个单位长度的速度运动,同时动点F从B开始沿BC向C以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为t秒.
(1)求反比例函数的表达式.
(2)当t=1时,在y轴上是否存在点D,使△DEF的周长最小?若存在,请求出△DEF的周长最小值;若不存在,请说明理由.
(3)在双曲线上是否存在一点M,使以点B、E、F、M为顶点的四边形是平行四边形?若存在,请求出满足条件t的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ;(3)存在,t=
;(3)存在,t=![]() 或t=2
或t=2
【解析】
(1)根据AB与BC的长,且B为第一象限角,确定出B的坐标,代入反比例函数解析式求出k的值,即可确定出反比例解析式;
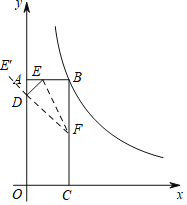
(2)运动1秒时,在y轴上存在点D,使△DEF的周长最小,理由为:作出E关于y轴的对称点E′,连接E′F,与y轴交于点D,连接DE,EF,此时△DEF周长最小,求出周长最小值即可;
(3)存在,若四变形BEMF为平行四边形,由题意得E(t,8),F(3,8-2t),0<t≤3.分BF为对角线,BE为对角线,EF为对角线时,建立方程求解即可得出结论.
解:(1)由题可知点B的坐标为(3,8),且点B在y=![]() 上.
上.
∴k=3×8=24,
∴反比例函数的表达式为:y=![]() .
.
(2)t=1时,E(1,8),F(3,6),则EF=![]() ,
,
取E关于y轴的对称E′(-1,8),
连接E′F,E′F=![]() ,△DEF的周长=DE+DF+EF=
,△DEF的周长=DE+DF+EF=![]() +DE′+DF≥2
+DE′+DF≥2![]() +E′F,
+E′F,
∴△DEF的周长的最小值=2![]() +2
+2![]() ,
,
此时点D为E′F与y轴交点,
∵E′(-1,8),F(3,6),
设E′F:y=kx+b,
则![]() ,
,
解得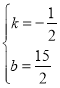 ,
,
∴E′F:y=![]() ,
,
∴此时D(0,![]() ),
),
即:y轴上存在点D(0,![]() ),使△DEF周长最小,且最小值为2
),使△DEF周长最小,且最小值为2![]() +2
+2![]() .
.
(3)存在,若四边形BEMF为平行四边形,由题意得E(t,8),F(3,8-2t),0<t≤3.
①当BF是对角线时,BE//FM,此时M在F右侧,M(![]() ,82t),
,82t),
又∵BE=FM,
∴3t=![]() 3,t2-10t+12=0,
3,t2-10t+12=0,
解得t1=5![]() ,t2=5+
,t2=5+![]() (舍).
(舍).
②当BE为对角线时,BF//EM,此时M在E正上方,Mt(t,![]() ),
),
∵ME=BF,
∴![]() 8=2t,t2+4t-12=0,
8=2t,t2+4t-12=0,
解得t1=2,t2=-6(舍).
③EF为对角线时,明显,点M不在双曲线上.
故综上:t=2或5![]() .
.