题目内容
如图,已知在Rt△ABC中,∠C=90°,它的三边长分别为a,b,c,对于同一个锐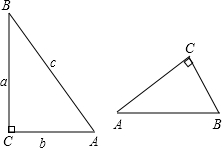 角A的正弦,余弦存在关系式sin2A+cos2A=1试说明.
角A的正弦,余弦存在关系式sin2A+cos2A=1试说明.
解:∵sinA=______,cosA=______.
∴sin2A+cos2A=______,
∵a2+b2=c2,∴sin2A+cos2A=1.
(1)在横线上填上适当内容;
(2)若∠α为锐角,利用(1)的关系式解决下列问题.
①若sinα=
,求cosα的值;cosα=
②若sinα+cosα=1.1,求sinαcosα的值.sinαcosα=0.105.
 角A的正弦,余弦存在关系式sin2A+cos2A=1试说明.
角A的正弦,余弦存在关系式sin2A+cos2A=1试说明.解:∵sinA=______,cosA=______.
∴sin2A+cos2A=______,
∵a2+b2=c2,∴sin2A+cos2A=1.
(1)在横线上填上适当内容;
(2)若∠α为锐角,利用(1)的关系式解决下列问题.
①若sinα=
| 4 |
| 5 |
| 3 |
| 5 |
②若sinα+cosα=1.1,求sinαcosα的值.sinαcosα=0.105.
(1)∵sinA=
,cosA=
.
∴sin2A+cos2A=
+
=
,
∵a2+b2=c2,∴sin2A+cos2A=1.
(2)∵sinα=
,sin2A+cos2A=1,
∴cosα=
=
=
.
(3)∵sinα+cosα=1.1,sin2A+cos2A=1,
∴(sinα+cosα)2=1.21,
sin2A+cos2A+2sincosα=1.21,
1+2sincosα=1.21,
∴sincosα=(1.21-1)÷2=0.105.
| a |
| c |
| b |
| c |
∴sin2A+cos2A=
| a2 |
| c2 |
| b2 |
| c2 |
| a2+b2 |
| c2 |
∵a2+b2=c2,∴sin2A+cos2A=1.
(2)∵sinα=
| 4 |
| 5 |
∴cosα=
| 1-sin2α |
1-(
|
| 3 |
| 5 |
(3)∵sinα+cosα=1.1,sin2A+cos2A=1,
∴(sinα+cosα)2=1.21,
sin2A+cos2A+2sincosα=1.21,
1+2sincosα=1.21,
∴sincosα=(1.21-1)÷2=0.105.

练习册系列答案
相关题目
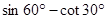 = ▲
= ▲