题目内容
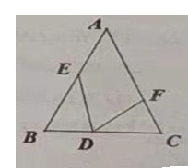
【题目】已知:如图,在△![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上的中线,
上的中线,![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)求证:![]() ;
;
(2)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .求证:
.求证:![]()
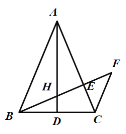
【答案】(1)见解析;(2)见解析
【解析】
(1)由三线合一可证BD=CD,然后通过证明△BDH∽△ADC,即可证明结论成立;
(2)连接CH,由等腰三角形的性质可证∠ABH=∠ACH.根据平行线的性质定理得到∠BFC=∠FBA,从而∠BFC=∠ECH;然后可证△CFH∽△ECH,并根据相似三角形的性质定理与等量代换得到结论.
(1)∵![]() ,
,![]() 是边
是边![]() 上的中线,
上的中线,
∴AD⊥BC,BD=CD,
∴∠ACD+∠CAD=90°.
∵![]() ,
,
∴∠EBD+∠ACB=90°,
∴∠CAD=∠CBD,
∵∠BDH=∠CDH=90°,
∴△BDH∽△ADC,
∴![]() ,
,
∴![]() ;
;
(2)如图所示,连接CH.
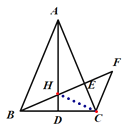
∵AD⊥BC,BD=CD,
∴AD垂直平分BC,
∴BH=CH,
∴∠HBD=∠HCD,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABH=∠ACH.
∵AB∥CF,
∴∠BFC=∠FBA.
∴∠BFC=∠ECH.
在△CFH与△ECH中,
∵∠BFC=∠ECH,∠CHE=∠CHF,
∴△CFH∽△ECH,
∴CH:HE=HF:CH.
又∵BH=CH,
∴BH2=HE·HF.

练习册系列答案
相关题目