ЬтФПФкШн
ЁОЬтФПЁПФГЪ§бЇПЮЭтаЫШЄаЁзщГЩдБдкбаОПЯТУцШ§ИігаСЊЯЕЕФЮЪЬтЃЌЧыФуАяжњЫћУЧНтОіЃК
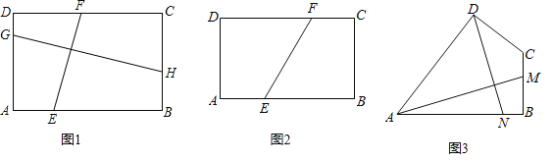
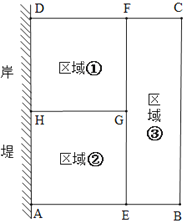
ЃЈ1ЃЉШчЭМ1ЃЌОиаЮABCDжаЃЌABЃНaЃЌBCЃНbЃЌЕуEЃЌFЗжБ№дкABЃЌDCЩЯЃЌЕуGЃЌHЗжБ№дкADЃЌBCЩЯЧвEFЁЭGHЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
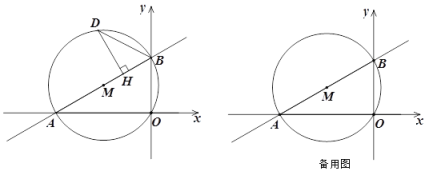
ЃЈ2ЃЉШчЭМ2ЃЌОиаЮABCDжаЃЌABЃН4ЃЌBCЃН3ЃЌНЋОиаЮЖделЃЌЪЙЕУBЁЂDжиЕўЃЌелКлЮЊEFЃЌЧѓEFЕФГЄЃЎ
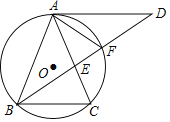
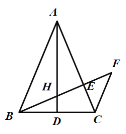
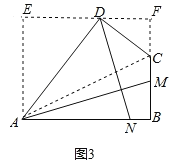
ЃЈ3ЃЉШчЭМ3ЃЌЫФБпаЮABCDжаЃЌЁЯABCЃН90ЁуЃЌABЃНADЃН8ЃЌBCЃНCDЃН4ЃЌAMЁЭDNЃЌЕуMЃЌNЗжБ№дкБпBCЃЌABЩЯЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1ЃЌЙ§ЕуGзїGMЁЭCBгкMЃЌЙ§ЕуEзїENЁЭCDгкЕуNЃЌПЩжЄЫФБпаЮDCMGЪЧОиаЮЃЌЫФБпаЮABMGЪЧОиаЮЃЌЫФБпаЮAENDЪЧОиаЮЃЌЫФБпаЮBCNEЪЧОиаЮЃЌПЩЕУGM=CD=ABЃЌEN=AD=BCЃЌЭЈЙ§жЄУїЁїEFNЁзЁїGHMЃЌПЩЧѓНтЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгBDНЛEFгкЕуOЃЌDEЃЌBFЃЌПЩжЄЫФБпаЮDFBEЪЧСтаЮЃЌПЩЕУBO=DOЃЌEO=FOЃЌBDЁЭEFЃЌгЩЙДЙЩЖЈРэПЩЧѓDEЃЌDOЃЌEOЕФГЄЃЌМДПЩЧѓEFЕФГЄЃЛ
ЃЈ3ЃЉЙ§ЕуDзїEFЁЭBCЃЌНЛBCЕФбгГЄЯпгкFЃЌЙ§ЕуAзїAEЁЭEFЃЌСЌНгACЃЌгЩЁАSSSЁБПЩжЄЁїACDЁеЁїACBЃЌПЩЕУЁЯADC=ЁЯABC=90ЁуЃЌЭЈЙ§жЄУїЁїADEЁзЁїDCFЃЌПЩЕУAE=2DFЃЌDE=2CFЃЌгЩЙДЙЩЖЈРэПЩЧѓDEЕФГЄЃЌМДПЩЧѓНтЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЙ§ЕуGзїGMЁЭCBгкMЃЌЙ§ЕуEзїENЁЭCDгкЕуNЃЌ
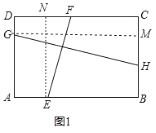
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрЁЯAЃНЁЯBЃНЁЯCЃНЁЯDЃН90ЁуЃЌABЃНCDЃЌADЃНBCЃЌЧвGMЁЭBCЃЌENЁЭCDЃЌ
ЁрЫФБпаЮDCMGЪЧОиаЮЃЌЫФБпаЮABMGЪЧОиаЮЃЌЫФБпаЮAENDЪЧОиаЮЃЌЫФБпаЮBCNEЪЧОиаЮЃЌ
ЁрGMЃНCDЃНABЃЌENЃНADЃНBCЃЌ
ЁпEFЁЭGHЃЌЁЯBCDЃН90ЁуЃЌ
ЁрЁЯEFC+ЁЯGHCЃН180ЁуЃЌЧвЁЯDFE+ЁЯEFCЃН180ЁуЃЌ
ЁрЁЯEFNЃНЁЯGHCЃЌЧвЁЯENFЃНЁЯGMHЃН90ЁуЃЌ
ЁрЁїEFNЁзЁїGHMЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгBDНЛEFгкЕуOЃЌDEЃЌBFЃЌ
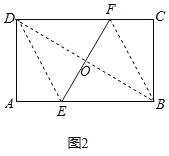
ЁпНЋОиаЮЖделЃЌЪЙЕУBЁЂDжиЕўЃЌ
ЁрBEЃНDEЃЌЁЯDEFЃНЁЯBEFЃЌ
ЁпABЁЮCDЃЌ
ЁрЁЯDFEЃНЁЯBEFЃЌ
ЁрЁЯDFEЃНЁЯDEFЃЌ
ЁрDFЃНDEЃЌЧвBEЃНDEЃЌ
ЁрBEЃНDFЃЌЧвABЁЮCDЃЌ
ЁрЫФБпаЮDFBEЪЧЦНааЫФБпаЮЃЌЧвDFЃНDEЃЌ
ЁрЫФБпаЮDFBEЪЧСтаЮЃЌ
ЁрBOЃНDOЃЌEOЃНFOЃЌBDЁЭEFЃЌ
ЁпDE2ЃНAE2+AD2ЃЌ
ЁрDE2ЃН9+ЃЈ4ЉDEЃЉ2ЃЌ
ЁрDEЃН![]() ЃЌ
ЃЌ
ЁпBDЃН![]() ЃН
ЃН![]() ЃН5ЃЌ
ЃН5ЃЌ
ЁрDOЃНBOЃН![]() ЃЌ
ЃЌ
ЁрOEЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрEFЃН2OEЃН![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЙ§ЕуDзїEFЁЭBCЃЌНЛBCЕФбгГЄЯпгкFЃЌЙ§ЕуAзїAEЁЭEFЃЌСЌНгACЃЌ
ЁпЁЯABCЃН90ЁуЃЌAEЁЭEFЃЌEFЁЭBCЃЌ
ЁрЫФБпаЮABFEЪЧОиаЮЃЌ
ЁрЁЯEЃНЁЯFЃН90ЁуЃЌAEЃНBFЃЌEFЃНABЃН8ЃЌ
ЁпADЃНABЃЌBCЃНCDЃЌACЃНACЃЌ
ЁрЁїACDЁеЁїACBЃЈSSSЃЉ
ЁрЁЯADCЃНЁЯABCЃН90ЁуЃЌ
ЁрЁЯADE+ЁЯCDFЃН90ЁуЃЌЧвЁЯADE+ЁЯEADЃН90ЁуЃЌ
ЁрЁЯEADЃНЁЯCDFЃЌЧвЁЯEЃНЁЯFЃН90ЁуЃЌ
ЁрЁїADEЁзЁїDCFЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAEЃН2DFЃЌDEЃН2CFЃЌ
ЁпDC2ЃНCF2+DF2ЃЌ
Ёр16ЃНCF2+ЃЈ8Љ2CFЃЉ2ЃЌ
ЁрDEЃН4ЃЈВЛКЯЬтвтЩсШЅЃЉЃЌDEЃН![]() ЃЌ
ЃЌ
ЁрBFЃНBC+CFЃН![]() ЃНAEЃЌ
ЃНAEЃЌ
гЩЃЈ1ЃЉПЩжЊЃК![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ