ЬтФПФкШн
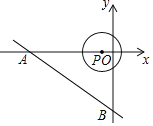
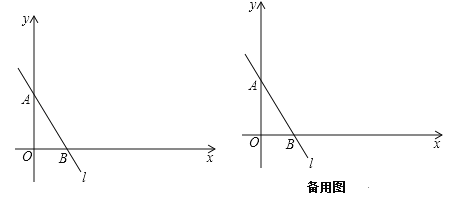
ЁОЬтФПЁПШчЭМЃЌвбжЊвЛДЮКЏЪ§y=Љ![]() x+4ЕФЭМЯѓЪЧжБЯпlЃЌЩшжБЯпlЗжБ№гыyжсЁЂxжсНЛгкЕуAЁЂBЃЎ
x+4ЕФЭМЯѓЪЧжБЯпlЃЌЩшжБЯпlЗжБ№гыyжсЁЂxжсНЛгкЕуAЁЂBЃЎ
ЃЈ1ЃЉЧѓЯпЖЮABЕФГЄЖШЃЛ
ЃЈ2ЃЉЩшЕуMдкЩфЯпABЩЯЃЌНЋЕуMШЦЕуAАДФцЪБеыЗНЯђа§зЊ90ЁуЕНЕуNЃЌвдЕуNЮЊдВаФЃЌNAЕФГЄЮЊАыОЖзїЁбNЃЎ
ЂйЕБЁбNгыxжсЯрЧаЪБЃЌЧѓЕуMЕФзјБъЃЛ
ЂкдкЂйЕФЬѕМўЯТЃЌЩшжБЯпANгыxжсНЛгкЕуCЃЌгыЁбNЕФСэвЛИіНЛЕуЮЊDЃЌСЌНгMDНЛxжсгкЕуEЃЌжБЯпmЙ§ЕуNЗжБ№гыyжсЁЂжБЯпlНЛгкЕуPЁЂQЃЌЕБЁїAPQгыЁїCDEЯрЫЦЪБЃЌЧѓЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉAB=5ЃЛЃЈ2ЃЉЂйM(6,-4)ЃЛЂкЃЈ0ЃЌ14ЃЉЛђЃЈ0ЃЌ-6ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩвЛДЮКЏЪ§НтЮіЪНШнвзЧѓЕУAЁЂBЕФзјБъЃЌРћгУЙДЙЩЖЈРэПЩЧѓЕУABЕФГЄЖШЃЛ
ЃЈ2ЃЉЂйИљОнЭЌНЧЕФШ§НЧКЏЪ§ЕУЃКtanЁЯOAB=![]() ЃЌЩшEM=3xЃЌAE=4xЃЌдђAM=5xЃЌЕУMЃЈ3xЃЌ-4x+4ЃЉЃЌжЄУїЁїAHNЁеЁїMEAЃЌдђAH=EM=3xЃЌИљОнNG=OHЃЌСаЪНПЩЕУxЕФжЕЃЌМЦЫуMЕФзјБъМДПЩЃЛ
ЃЌЩшEM=3xЃЌAE=4xЃЌдђAM=5xЃЌЕУMЃЈ3xЃЌ-4x+4ЃЉЃЌжЄУїЁїAHNЁеЁїMEAЃЌдђAH=EM=3xЃЌИљОнNG=OHЃЌСаЪНПЩЕУxЕФжЕЃЌМЦЫуMЕФзјБъМДПЩЃЛ
ЂкШчЭМ2ЃЌЯШМЦЫуEгыGжиКЯЃЌвзЕУЁЯQAP=ЁЯOAB=ЁЯDCEЃЌЫљвдЁїAPQгыЁїCDEЯрЫЦЪБЃЌЖЅЕуCБигыЖЅЕуAЖдгІЃЌПЩЗжСНжжЧщПіНјааЬжТлЃК
iЃЉЕБЁїDCEЁзЁїQAPЪБЃЌжЄУїЁїACOЁзЁїNCEЃЌСаБШР§ЪНПЩЕУCO=![]() ЃЌИљОнШ§НЧКЏЪ§ЕУЃКtanЁЯQNA=tanЁЯDNF=
ЃЌИљОнШ§НЧКЏЪ§ЕУЃКtanЁЯQNA=tanЁЯDNF=![]() ЃЌAQ=20ЃЌдђtanЁЯQAH=tanЁЯOAB=
ЃЌAQ=20ЃЌдђtanЁЯQAH=tanЁЯOAB=![]() ЃЌЩшQH=3xЃЌAH=4xЃЌдђAQ=5xЃЌЧѓГіxЕФжЕЃЌЕУPЃЈ0ЃЌ14ЃЉЃЛ
ЃЌЩшQH=3xЃЌAH=4xЃЌдђAQ=5xЃЌЧѓГіxЕФжЕЃЌЕУPЃЈ0ЃЌ14ЃЉЃЛ
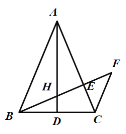
iiЃЉЕБЁїDCEЁзЁїPAQЪБЃЌШчЭМ3ЃЌЯШжЄУїBгыQжиКЯЃЌгЩAN=APПЩЕУPЃЈ0ЃЌ-6ЃЉЃЎ
ЃЈ1ЃЉЕБx=0ЪБЃЌy=4ЃЌ
ЁрAЃЈ0ЃЌ4ЃЉЃЌ
ЁрOA=4ЃЌ
ЕБy=0ЪБЃЌ-![]() x+4=0ЃЌ
x+4=0ЃЌ
x=3ЃЌ
ЁрBЃЈ3ЃЌ0ЃЉЃЌ
ЁрOB=3ЃЌ
гЩЙДЙЩЖЈРэЕУЃКAB=5ЃЛ
ЃЈ2ЃЉЂйШчЭМ1ЃЌЙ§NзїNHЁЭyжсгкHЃЌЙ§MзїMEЁЭyжсгкEЃЌ
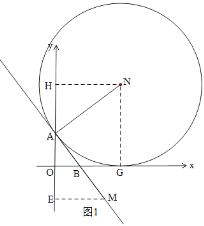
tanЁЯOAB=![]() ЃЌ
ЃЌ
ЁрЩшEM=3xЃЌAE=4xЃЌдђAM=5xЃЌ
ЁрMЃЈ3xЃЌ-4x+4ЃЉЃЌ
гЩа§зЊЕУЃКAM=ANЃЌЁЯMAN=90ЁуЃЌ
ЁрЁЯEAM+ЁЯHAN=90ЁуЃЌ
ЁпЁЯEAM+ЁЯAME=90ЁуЃЌ
ЁрЁЯHAN=ЁЯAMEЃЌ
ЁпЁЯAHN=ЁЯAEM=90ЁуЃЌ
ЁрЁїAHNЁеЁїMEAЃЌ
ЁрAH=EM=3xЃЌ
ЁпЁбNгыxжсЯрЧаЃЌЩшЧаЕуЮЊGЃЌСЌНгNGЃЌдђNGЁЭxжсЃЌ
ЁрNG=OHЃЌ
дђ5x=3x+4ЃЌ
2x=4ЃЌ
x=2ЃЌ
ЁрMЃЈ6ЃЌ-4ЃЉЃЛ
ЂкШчЭМ2ЃЌгЩЂйжЊNЃЈ8ЃЌ10ЃЉЃЌ
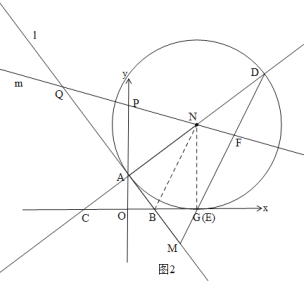
ЁпAN=DNЃЌAЃЈ0ЃЌ4ЃЉЃЌ
ЁрDЃЈ16ЃЌ16ЃЉЃЌ
ЩшжБЯпDMЃКy=kx+bЃЌ
АбDЃЈ16ЃЌ16ЃЉКЭMЃЈ6ЃЌ-4ЃЉДњШыЕУЃК
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпDMЕФНтЮіЪНЮЊЃКy=2x-16ЃЌ
ЁпжБЯпDMНЛxжсгкEЃЌ
ЁрЕБy=0ЪБЃЌ2x-16=0ЃЌ
x=8ЃЌ
ЁрEЃЈ8ЃЌ0ЃЉЃЌ
гЩЂйжЊЃКЁбNгыxжсЯрЧаЃЌЧаЕуЮЊGЃЌЧвGЃЈ8ЃЌ0ЃЉЃЌ
ЁрEгыЧаЕуGжиКЯЃЌ
ЁпЁЯQAP=ЁЯOAB=ЁЯDCEЃЌ
ЁрЁїAPQгыЁїCDEЯрЫЦЪБЃЌЖЅЕуCБигыЖЅЕуAЖдгІЃЌ
ЗжСНжжЧщПіЃК
iЃЉЕБЁїDCEЁзЁїQAPЪБЃЌШчЭМ2ЃЌЁЯAQP=ЁЯNDEЃЌ
ЁпЁЯQNA=ЁЯDNFЃЌ
ЁрЁЯNFD=ЁЯQAN=90ЁуЃЌ
ЁпAOЁЮNEЃЌ
ЁрЁїACOЁзЁїNCEЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрCO=![]() ЃЌ
ЃЌ
СЌНгBNЃЌ
ЁрAB=BE=5ЃЌ
ЁпЁЯBAN=ЁЯBEN=90ЁуЃЌ
ЁрЁЯANB=ЁЯENBЃЌ
ЁпEN=NDЃЌ
ЁрЁЯNDE=ЁЯNEDЃЌ
ЁпЁЯCNE=ЁЯNDE+ЁЯNEDЃЌ
ЁрЁЯANB=ЁЯNDEЃЌ
ЁрBNЁЮDEЃЌ
RtЁїABNжаЃЌBN=![]() ЃЌ
ЃЌ
sinЁЯANB=ЁЯNDE=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрNF=2![]() ЃЌ
ЃЌ
ЁрDF=4![]() ЃЌ
ЃЌ
ЁпЁЯQNA=ЁЯDNFЃЌ
ЁрtanЁЯQNA=tanЁЯDNF=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAQ=20ЃЌ
ЁпtanЁЯQAH=tanЁЯOAB=![]() ЃЌ
ЃЌ
ЩшQH=3xЃЌAH=4xЃЌдђAQ=5xЃЌ
Ёр5x=20ЃЌ
x=4ЃЌ
ЁрQH=3x=12ЃЌAH=16ЃЌ
ЁрQЃЈ-12ЃЌ20ЃЉЃЌ
ЭЌРэвзЕУЃКжБЯпNQЕФНтЮіЪНЃКy=-![]() x+14ЃЌ
x+14ЃЌ
ЁрPЃЈ0ЃЌ14ЃЉЃЛ
iiЃЉЕБЁїDCEЁзЁїPAQЪБЃЌШчЭМ3ЃЌ
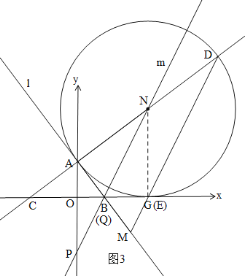
ЁрЁЯAPN=ЁЯCDEЃЌ
ЁпЁЯANB=ЁЯCDEЃЌ
ЁпAPЁЮNGЃЌ
ЁрЁЯAPN=ЁЯPNEЃЌ
ЁрЁЯAPN=ЁЯPNE=ЁЯANBЃЌ
ЁрBгыQжиКЯЃЌ
ЁрAN=AP=10ЃЌ
ЁрOP=AP-OA=10-4=6ЃЌ
ЁрPЃЈ0ЃЌ-6ЃЉЃЛ
злЩЯЫљЪіЃЌЁїAPQгыЁїCDEЯрЫЦЪБЃЌЕуPЕФзјБъЕФзјБъЃЈ0ЃЌ14ЃЉЛђЃЈ0ЃЌ-6ЃЉЃЎ