Question

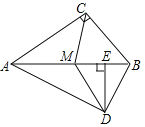
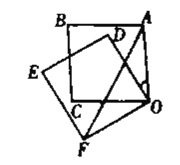
【题目】如图，边长为1的正方形OABC绕着点O逆时针旋转30°得到正方形ODEF，连接AF，求的周长.

Answer 1

【答案】2+

【解析】

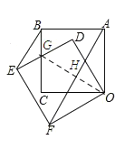
记BC与ED的交点为G，连结OG交AF与点H，延长OG交BE与点M．首先依据HL可证明Rt△OCG≌Rt△ODG，则CD＝CG，∠COG＝∠DOG，于是可得到BG＝EG，OH为∠AOF的平分线，则AH＝FH，然后利用特殊锐角三角函数值可求得AH的长，从而可求得AF的长，从而可求得的周长．

记BC与ED的交点为G，连结OG交AF与点H．

∵∠D＝∠C＝90°，

∴△OCG和△ODG均为直角三角形．

又∵，

∴Rt△OCG≌Rt△ODG．

∴DG＝CG，∠COG＝∠DOG．

∴BG＝EG．

又∵∠AOD＝∠FOC，

∴∠FOH＝∠AOH＝∠AOF＝60°．

又∵OA＝OF，

∴AH＝FH＝AOsin60°=1×=，

∴AF＝2AH=

∴的周长=AO+FO+AF=1+1+=2+.