题目内容
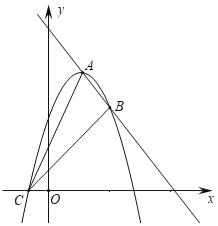
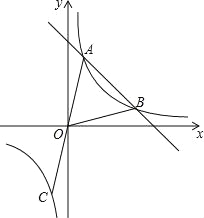
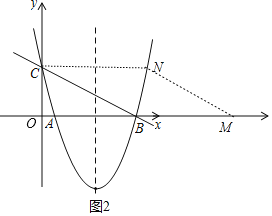
【题目】如图,抛物线![]() 与x轴相交于A,B两点,与y轴相交于点C,已知抛物线的对称轴所在的直线是
与x轴相交于A,B两点,与y轴相交于点C,已知抛物线的对称轴所在的直线是![]() ,点B的坐标为
,点B的坐标为![]()
![]() 抛物线的解析式是______;
抛物线的解析式是______;
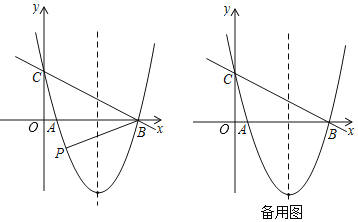
![]() 若点P是直线BC下方抛物线上一动点,当
若点P是直线BC下方抛物线上一动点,当![]() 时,求出点P的坐标;
时,求出点P的坐标;
![]() 若M为x轴上一动点,在抛物线上是否存在点N,使得点B,C,M,N构成的四边形是菱形?若存在,求出N点的坐标;若不存在,请说明理由.
若M为x轴上一动点,在抛物线上是否存在点N,使得点B,C,M,N构成的四边形是菱形?若存在,求出N点的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 点坐标为
点坐标为![]() ;(3)在抛物线上不存在点N,使得点B,C,M,N构成的四边形是菱形,见解析.
;(3)在抛物线上不存在点N,使得点B,C,M,N构成的四边形是菱形,见解析.
【解析】
(1)利用抛物线对称性得到点A(![]() ,0),然后利用交点式写出抛物线解析式;
,0),然后利用交点式写出抛物线解析式;
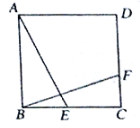
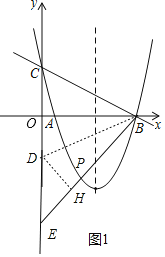
(2)如图,∠ABP=2∠ABC,直线BP交y轴于E,作C点关于x轴的对称轴点D,DH⊥BE于H,则∠ABC=∠ABD,∠ABD=∠PBD,则OD=DH=2,设DE=t,利用相似比表示出EH=1+![]() t,根据勾股定理得到22+(1+
t,根据勾股定理得到22+(1+![]() t)2=t2,解得t1=﹣2,t2=
t)2=t2,解得t1=﹣2,t2=![]() ,从而得到E(0,
,从而得到E(0,![]() ),利用待定系数法得直线BE的解析式为y=
),利用待定系数法得直线BE的解析式为y=![]() x﹣
x﹣![]() ,然后解方程组
,然后解方程组 得P点坐标;
得P点坐标;
(3)若BC为对角线,易得点B,C,M,N构成的四边形不是菱形;若BC为边,则CN∥BM,则CN=![]() ,而BC=2
,而BC=2![]() ,利用BC≠CN可判断点B,C,M,N构成的四边形不可能为菱形.
,利用BC≠CN可判断点B,C,M,N构成的四边形不可能为菱形.
解:![]() 点A与点
点A与点![]() 关于直线是
关于直线是![]() ,
,
![]() 点
点![]() ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ,
,
即![]() ;
;
故答案为![]() ;
;
![]() 如图,
如图,![]() ,
,
直线BP交y轴于E,作C点关于x轴的对称轴点D,![]() 于H,
于H,
则![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
![]() ,
,
设![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,即
,即![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,解得
,解得![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
设直线BE的解析式为![]() ,
,
把![]() ,
,![]() 代入得
代入得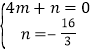 ,
,
![]() 直线BE的解析式为
直线BE的解析式为![]() ,
,
解方程组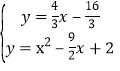 得
得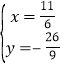 或
或![]() ,
,
![]() 点坐标为
点坐标为![]() ;
;
![]() 在抛物线上不存在点N,使得点B,C,M,N构成的四边形是菱形.
在抛物线上不存在点N,使得点B,C,M,N构成的四边形是菱形.
理由如下:
若BC为对角线,易得点B,C,M,N构成的四边形不是菱形;
若BC为边,则![]() ,则
,则![]() ,而
,而![]() ,所以点B,C,M,N构成的四边形不可能为菱形.
,所以点B,C,M,N构成的四边形不可能为菱形.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案