题目内容
【题目】已知等边三角形ABC．如图，
（1）分别以点A，B为圆心，大于的
AB长为半径作弧，两弧相交于M，N两点；
（2）作直线MN交AB于点D；
（2）分别以点A，C为圆心，大于AC的长为半径作弧，两弧相交于H，L两点；
（3）作直线HL交AC于点E；
（4）直线MN与直线HL相交于点O；
（5）连接OA，OB，OC．
根据以上作图过程及所作图形，下列结论：①OB＝2OE；②AB＝2OA；③OA＝OB＝OC；④∠DOE＝120°，正确的是（ ）
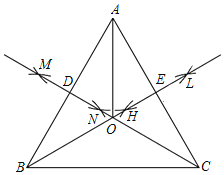
A.①②③④B.①③④C.①②③D.③④
【答案】B
【解析】
根据等边三角形的性质，三角形的外心，三角形的内心的性质一一判断即可．
解：由作图可知，点O是△ABC的外心，
∵△ABC是等边三角形，
∴点O是△ABC的外心也是内心，
∴OB＝2OE，OA＝OB＝OC，
∵∠BAC＝60°，∠ADO＝∠AEO＝90°，
∴∠DOE＝180°﹣60°＝120°，
故①③④正确，
故选：B．
练习册系列答案
相关题目
