��Ŀ����
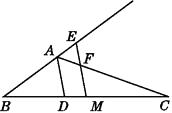
����Ŀ�����dz����ij��˹����Ƕ����������棬�������ĺ��ĵ��ݶ�����������������϶��ɵķ��ͼ�Σ��������Ϊ��������������ֱ��Ϊ6dm������3dm�����Ǹ�1dm������ֱ�������ֱ����Ϊ��ͬ��������ֱ������ϵ��ͼ����ʾ��ͼ���DZ���ͼ��������ѹ��ݶ����������ΪC1���ѹ����ݶ����������ΪC2��
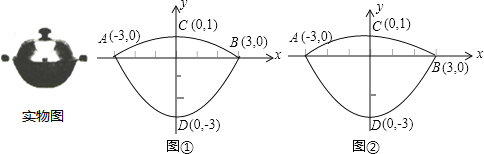
��1����C1��C2�Ľ���ʽ��
��2���������ʱ����ˮλ�߶���1dm�����ʱˮ���ֱ����
��3�������һ������ֱ��Ϊ3dm���߶�Ϊ3dm��Բ����������보�˹�����ʳ������ܷ��������ϣ���˵�����ɣ�
���𰸡���1��������C1��y=![]() x2��3����3��x��3����������C2��y=��
x2��3����3��x��3����������C2��y=��![]() x2+1����3��x��3������2��2
x2+1����3��x��3������2��2![]() dm����3���������������ϣ����ɼ�����.
dm����3���������������ϣ����ɼ�����.
�������������������1����֪A��B��C��D�ĵ����꣬���ô���ϵ��������ȷ���������Ľ���ʽ��
��2�����˹����ˮλ�߶�Ϊ1dm��y=-2���з������x��ֵ���ɵô𰸣�
��3������ֱ��Ϊ3dm���߶�Ϊ3dmԲ���������ܷ������ڣ����жϵ�x=![]() ʱ��C1��C2�е�yֵ�IJ���3�Ƚϴ�С���Ӷ��ɵô𰸣�
ʱ��C1��C2�е�yֵ�IJ���3�Ƚϴ�С���Ӷ��ɵô𰸣�
�⣺��1������������C1��C2������A����3��0����B��3��0�����������ǵĽ���ʽΪ��y=a��x��3����x+3����
������C1������D��0����3����
���У���3=a��0��3����0+3������ã�a=![]()
����������C1��y=![]() x2��3����3��x��3����
x2��3����3��x��3����
������C2������C��0��1����
���У�1=a��0��3����0+3������ã�a=��![]()
����������C2��y=��![]() x2+1����3��x��3����
x2+1����3��x��3����
��2�������˹����ˮλ�߶�Ϊ1dmʱ��y=��2����![]() x2��3=��2��
x2��3=��2��
��ã�x=��![]() ��
��
���ʱˮ���ֱ��Ϊ2![]() dm��
dm��
��3���������������ϣ��������£�
��x=![]() ʱ��������C1��y=
ʱ��������C1��y=![]() ����
����![]() ��2��3=��
��2��3=��![]() ��������C2��y=��
��������C2��y=��![]() ����
����![]() ��2+1=
��2+1=![]() ��
��
��![]() ������
������![]() ��=3��
��=3��
���������������.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ������2����֯��һ�ξ����ж����������������10�˵ı����ɼ����±���10 ���ƣ���
�� | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
�� | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
�ټ������ݵ���λ���� �� �������ݵ���������
�ڼ����������ݵ�ƽ����������
����֪�������ݵķ�����1.4��2 �� ��ɼ���Ϊ������� ��