题目内容
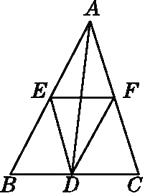
【题目】如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.求证: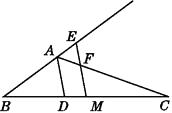
(1)AE=AF;
(2)BE= ![]() (AB+AC).
(AB+AC).
【答案】
(1)证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵AD∥EM,
∴∠BAD=∠AEF,∠CAD=∠AFE.
∴∠AEF=∠AFE.
∴AE=AF.
(2)证明:如图,在BE的延长线上截取EG=BE,并连接CG.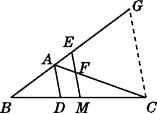
∵BM=CM,∴EM为△BCG的中位线.
∴EM∥CG.∴∠AGC=∠AEF,∠ACG=∠AFE.
∵∠AEF=∠AFE,
∴∠AGC=∠ACG.
∴AG=AC.
∴BE= ![]() BG=
BG= ![]() (AB+AG)=
(AB+AG)= ![]() (AB+AC)
(AB+AC)
【解析】(1)根据角平分线的定义得出∠BAD=∠CAD,再根据平行线的性质得出∠BAD=∠AEF,∠CAD=∠AFE,就可证得∠AEF=∠AFE,然后根据等边对等角即可证得结论。
(2)在BE的延长线上截取EG=BE,并连接CG,构造△ACG的中位线得出EM∥CG,根据平行线的性质证得∠AGC=∠AEF,∠ACG=∠AFE,再根据∠AEF=∠AFE,从而得到∠AGC=∠ACG,根据等角对等边证出AG=AC,然后根据BE= ![]() BG,就可证得结论。
BG,就可证得结论。

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目