题目内容
有下列四个命题:
①两边和其中一边上的高对应相等的两个三角形一定是全等三角形.
②两边和第三边上的高对应相等的两个锐角三角形不一定是全等三角形.
③两边和第三边上的高对应相等的两个三角形是全等三角形.
④两边和其中一边所对的角对应相等的两个三角形不一定是全等三角形.其中正确的是( )
①两边和其中一边上的高对应相等的两个三角形一定是全等三角形.
②两边和第三边上的高对应相等的两个锐角三角形不一定是全等三角形.
③两边和第三边上的高对应相等的两个三角形是全等三角形.
④两边和其中一边所对的角对应相等的两个三角形不一定是全等三角形.其中正确的是( )
分析:根据全等三角形的判定定理,分别对选项一一判断,举出反例即可.
解答:解:①正确,如图:

在锐角△ABC与锐角△A1B1C1中,AB=A1B1,BC=B1C1,AD⊥BC,A1D1⊥B1C1,且AD=A1D1.可先证得
△ADB≌△A1D1B1,即可证得△ABC≌△A1B1C1;
②不正确,如图:

在锐角△ABC与锐角△A1B1C1中,AB=A1B1,AC=A1C1,AD⊥BC,A1D1⊥B1C1,且AD=A1D1.可先证得
△ADB≌△A1D1B1,△ADC≌△A1D1C1,即可证得△ABC≌△A1B1C1;
③不正确,举一反例说明,如图:
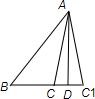
在钝角△ABC与锐角△ABC1中,AB=AB,AC=AC1,AD⊥BC1,AD=AD.但△ABC与△ABC1显然是不全等的;
④正确,可举一例说明,如图:
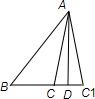
在钝角△ABC与锐角△ABC1中,AB=AB,AC=AC1,∠ABC=∠ABC1,但△ABC与△ABC1显然是不全等的.
所以正确的是①④.
故选D.

在锐角△ABC与锐角△A1B1C1中,AB=A1B1,BC=B1C1,AD⊥BC,A1D1⊥B1C1,且AD=A1D1.可先证得
△ADB≌△A1D1B1,即可证得△ABC≌△A1B1C1;
②不正确,如图:

在锐角△ABC与锐角△A1B1C1中,AB=A1B1,AC=A1C1,AD⊥BC,A1D1⊥B1C1,且AD=A1D1.可先证得
△ADB≌△A1D1B1,△ADC≌△A1D1C1,即可证得△ABC≌△A1B1C1;
③不正确,举一反例说明,如图:

在钝角△ABC与锐角△ABC1中,AB=AB,AC=AC1,AD⊥BC1,AD=AD.但△ABC与△ABC1显然是不全等的;
④正确,可举一例说明,如图:

在钝角△ABC与锐角△ABC1中,AB=AB,AC=AC1,∠ABC=∠ABC1,但△ABC与△ABC1显然是不全等的.
所以正确的是①④.
故选D.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目