题目内容
【题目】如图，已知菱形ABCD边长为4，
，点E从点A出发沿着AD、DC方向运动，同时点F从点D出发以相同的速度沿着DC、CB的方向运动．
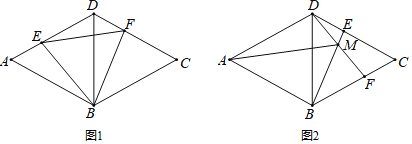
如图1，当点E在AD上时，连接BE、BF，试探究BE与BF的数量关系，并证明你的结论；
在的前提下，求EF的最小值和此时
的面积；
当点E运动到DC边上时，如图2，连接BE、DF，交点为点M，连接AM，则
大小是否变化？请说明理由．
【答案】
，证明见解析；
的最小值是
，
；
如图3，当点E运动到DC边上时，
大小不发生变化，理由见解析.
【解析】
先证明
和
是等边三角形，再证明
≌
，可得结论；
由≌
，易证得
是正三角形，继而可得当动点E运动到当
，即E为AD的中点时，BE的最小，根据等边三角形三线合一的性质可得BE和EF的长，并求此时的面积；
同理得：
≌
，则可得
，所以
，则A、B、M、D四点共圆，可得
．
，
证明：
、F的速度相同，且同时运动，
，
又
四边形ABCD是菱形，
，
，
，
是等边三角形，
同理也是等边三角形，
，
在和中，
，
≌，
；
由得：≌，
，
，
，
是等边三角形，
，
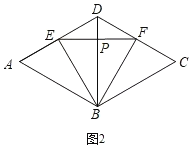
如图2，当动点E运动到，即E为AD的中点时，BE的最小，此时EF最小，
，
，
，
的最小值是，
中，
，
，
，
，
；
如图3，当点E运动到DC边上时，大小不发生变化，
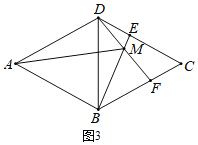
在和
中，
，
≌，
，
，
，
，
，
，
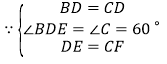、B、M、D四点共圆，
．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
