题目内容
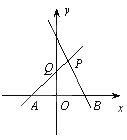
【题目】已知△ABC，AB=AC，∠BAC=∠EPF=90°，点P是BC的中点，两边PE、PF分别交AB，AC于E、F,连接EF、AP.有下列结论①AE=CF ②EF=AP ③△EPF是等腰直角三角形④
，其中正确的有( )个
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】分析：判断出
≌
，可得①③结论正确，同理证明
≌
即可得到④正确；
详解：
∴AP⊥BC，
∴
∴
∵
∴∠APE=∠CPF，
在等腰直角三角形ABC中，AP⊥BC，
∴
在△APE和△CPF中
∴△APE≌△CPF，
∴
∵
∴△EPF是等腰直角三角形；
即：①③正确；
同理：△APF≌△BPE，
∴
∴S四边形AEPF=
即：④正确；
∵△△EPF是等腰直角三角形，
∴
当PE⊥AB时,
而PE不一定垂直于AB，
∴AP不一定等于EF，
∴②错误；
故选C.
阅读快车系列答案【题目】大学生小张利用暑假50天在一超市勤工俭学，被安排销售一款成本为40元/件的新型商品，此类新型商品在第x天的销售量p件与销售的天数x的关系如下表：
x（天） | 1 | 2 | 3 | … | 50 |
p（件） | 118 | 116 | 114 | … | 20 |
销售单价q（元/件）与x满足：当1≤x＜25时q=x+60；当25≤x≤50时q=40+ 
．
（1）请分析表格中销售量p与x的关系，求出销售量p与x的函数关系．
（2）求该超市销售该新商品第x天获得的利润y元关于x的函数关系式．
（3）这50天中，该超市第几天获得利润最大？最大利润为多少？
【题目】某公交公司有A、B型两种客车，它们的载客量和租金如下表：
A | B | |
载客量（人/辆） | 45 | 30 |
租金 （元/辆） | 400 | 280 |
红星中学根据实际情况，计划租用A、B型客车共5辆，同时送八年级师生到基地参加社会实践活动.设租用A型客车x辆，根据要求回答下列问题.
（1）若要保证租车费用不超过1900元，求x的最大值；
（2）在（1）的条件下，若八年级师生共有195人，请设计一种最省钱的租车方案．
【题目】二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论：
（1）ac＜0；
（2）当x＞1时，y的值随x值的增大而减小．
（3）3是方程ax2+（b﹣1）x+c=0的一个根；
（4）当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0．
其中正确的个数为（ ）
A.4个
B.3个
C.2个
D.1个
