Question

【题目】在平面直角坐标系中，直线 y1＝kx+b 经过点 P（4，4）和点 Q（0，﹣4），与 x 轴交于点 A，与直线 y2＝mx+n 交于点 P．

（1）求出直线 y1＝kx+b 的解析式；

（2）求出点 A 的坐标；

（3）直线 y2＝mx+n 绕着点 P 任意旋转，与 x 轴交于点 B，当△PAB 是等腰三角形时，直接写出点B 的坐标．

Answer 1

【答案】（1）y1=2x4；（2）A(2,0)；（3）点B有4种位置使得△PAB为等腰三角形,坐标分别为(+2,0)、(2,0) 、(6,0)、(7,0).

【解析】

（1）利用待定系数法确定函数解析式；

（2）令y=0，可求解；

（3）对于本题中的等腰△PAB的腰不确定，需要分类讨论，分三种情况：PA=AB，AB=BP，AP=BP解答．

(1)把P(4,4)和点Q(0,4)分别代入y1=kx+b，得

，

解得

则直线y1=kx+b的解析式为：y1=2x4；

(2)∵直线y1=2x4与x轴交于点A，

∴当y=0时，0=2x4

∴x=2，

∴点A(2,0)；

(3)过点P作PM⊥x轴，交于点M，

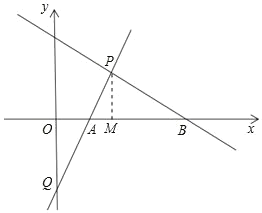
由题意可知A(2,0),M(4,0),AP=，AM=2

① 当AP=AB时,AB=，

∴B(2-,0)或者B(2+,0).

② 当PA=PB时，AB=2AM=4，

∴B(6,0)

③当PB=AB时,设AB=x,由勾股定理可得：42+（x-2）2=x2，

解得x=5，

∴B(7,0)

综上所述,点B有4种位置使得△PAB为等腰三角形,坐标分别为(+2,0)、(2,0) 、(6,0)、(7,0).