��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪����ABCD����������B��1��0����C��3��0����D��3��4������AΪ�����������y=ax2+bx+c����C������P�ӵ�A���������߶�AB���B�˶���ͬʱ����Q�ӵ�C���������߶�CD���D�˶�����P��Q���˶��ٶȾ�Ϊÿ��1����λ���˶�ʱ��Ϊt�룮����P��PE��AB��AC�ڵ�E��

��1��ֱ��д����A�����꣬����������ߵĽ���ʽ��
��2������E��EF��AD��F�����������ڵ�G����tΪ��ֵʱ����ACG�����������ֵΪ���٣�
��3���ڶ���P��Q�˶��Ĺ����У���tΪ��ֵʱ���ھ���ABCD�ڣ������߽磩���ڵ�H��ʹ��C��Q��E��HΪ������ı���Ϊ���Σ���ֱ��д��t��ֵ��
���𰸡���1��A��1��4����y=��x2+2x+3����2����t=2ʱ��S��ACG�����ֵΪ1����3��t=20��8![]() ��t=
��t=![]() ��
��
�������������������1�����ݾ��ε����ʿ���д����A�õ����ꣻ�ɶ���A���������������ߵĶ���ʽ����Ϊy=a��x-1��2+4��Ȼ��C��������룬�������ϵ��a��ֵ�����ô���ϵ�����������ߵĽ���ʽ������2�����ô���ϵ�������ֱ��AC�ķ���y=-2x+6����ͼ��������任������õ�P�����꣨1��4-t�����ݴ˿�����õ�E�������꣬�������ֱ��AC���̿�����õ�E���G�ĺ����ꣻȻ���������߷��̡�ͼ��������任�������GE=4-![]() ����A��GE�ľ���Ϊ��C��GE�ľ���Ϊ2-
����A��GE�ľ���Ϊ��C��GE�ľ���Ϊ2-![]() �������������ε������ʽ�������S��ACG=S��AEG+S��CEG=-
�������������ε������ʽ�������S��ACG=S��AEG+S��CEG=-![]() ��t-2��2+1���ɶ��κ�������ֵ���Խ��t=2ʱ��S��ACG�����ֵΪ1����3����Ϊ�������ڱ���ȵ�ƽ���ı��Σ����Ե�H��ֱ��EF�ϣ�
��t-2��2+1���ɶ��κ�������ֵ���Խ��t=2ʱ��S��ACG�����ֵΪ1����3����Ϊ�������ڱ���ȵ�ƽ���ı��Σ����Ե�H��ֱ��EF�ϣ�
���������
(1)A(1��4).
������֪�����������߽���ʽΪy=a(x1)2+4��
�������߹���C(3��0)��
��0=a(31)2+4��
��ã�a=1��
�������ߵĽ���ʽΪy=(x1)2+4,��y=x2+2x+3.
(2)��A(1��4)��C(3��0)��
�����ֱ��AC�Ľ���ʽΪy=2x+6.
�ߵ�P(1��4t).
�ཫy=4t����y=2x+6��,��õ�E�ĺ�����Ϊx=1+![]() .
.
���G�ĺ�����Ϊ1+![]() �����������ߵĽ���ʽ���������G��������Ϊ4
�����������ߵĽ���ʽ���������G��������Ϊ4![]() .
.
��GE=(4![]() )(4t)=t
)(4t)=t![]() .
.
�֡ߵ�A��GE�ľ���Ϊ![]() ,C��GE�ľ���Ϊ2
,C��GE�ľ���Ϊ2![]() ��
��
��S��ACG=S��AEG+S��CEG=![]() EG
EG![]() +
+![]() EG(2
EG(2![]() )
)
=![]() 2(t
2(t![]() )=
)=![]() (t2)2+1.
(t2)2+1.
��t=2ʱ��S��ACG�����ֵΪ1.
(3)��һ�������ͼ1��ʾ,��H��AC���Ϸ�,���ı���CQEH������֪CQ=CE=t,

������APE�ס�ABC��֪
![]() ����
����![]() �����t=20
�����t=20![]() ��
��
�ڶ��������ͼ2��ʾ��
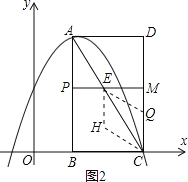
��H��AC���·������ı���CQHE������֪CQ=QE=EH=HC=t��PE=![]() t,EM=2
t,EM=2![]() t��MQ=42t.
t��MQ=42t.
����ֱ��������EMQ��,���ݹ��ɶ���֪EM2+MQ2=EQ2,��(2![]() t)2+(42t)2=t2��
t)2+(42t)2=t2��
���,t1=![]() ,t2=4(��������,��ȥ).
,t2=4(��������,��ȥ).
��������,t=20![]() ��t=
��t=![]() .
.