题目内容
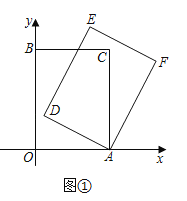
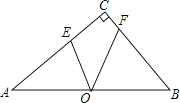
【题目】如图,Rt△ACB中,∠ACB=90°,O为AB的中点,AE=AO,BF=BO,OE=2![]() ,OF=3,则AB的长为( )
,OF=3,则AB的长为( )
A.![]() B.5C.8D.
B.5C.8D.![]()
【答案】A
【解析】
延长FO至H,使OH=OF,连接AH,EH,利用全等三角形的判定和性质可证得BF=AH=AE=AO=OB,再利用勾股定理解答即可.
解:延长FO至H,使OH=OF,连接AH,EH,
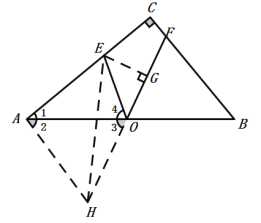
∵AO=OB,OH=OF,∠AOH=∠BOF,
在△AOH与△BOF中,
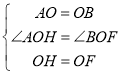 ,
,
∴△AOH≌△BOF(SAS),
∴BF=AH=AE=AO=OB,
∴∠2=∠B,
∴∠1+∠B=∠1+∠2=90![]() ,
,
∠3=∠AHO=![]() ,
,
∠4=∠AEO=![]() ,
,
∴∠3+∠4=![]()
=180![]() -
-![]() =135
=135![]() ,
,
过E作EG⊥FH,在Rt△EOG中,∠EOG=45![]() ,EO=2
,EO=2![]() ,
,
∴OG=EG=2,
∴HG=3+2=5,
∴![]() ,
,
在Rt△EAH中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故选:A.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目