题目内容
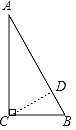
【题目】如图在直角三角形ABC中,边AC长4cm,边BC长3cm,边AB长5cm.
(1)三角形绕着边AC旋转一周,所得几何体的体积和绕着边BC旋转一周所得几何体体积是否一样?通过计算说明;
(2)若绕着边AB旋转一周,所得的几何体的体积是多少?

【答案】(1)三角形绕着边AC旋转一周,所得几何体的体积和绕着边BC旋转一周所得几何的体积不一样;(2)9.6πcm2
【解析】
(1)先分别求出旋转后得出的圆锥的体积,再比较即可;
(2)求出直角△ABC的高CD,再求出圆锥的体积即可.
(1)三角形绕着边AC旋转一周,所得几何体的体积是![]() ×π×32×4=12π(cm)2;
×π×32×4=12π(cm)2;
三角形绕着边BC旋转一周,所得几何体的体积是![]() ×π×42×3=16π(cm)2;
×π×42×3=16π(cm)2;
∵12π≠16π,
∴三角形绕着边AC旋转一周,所得几何体的体积和绕着边BC旋转一周所得几何的体积不一样;
(2)过C作CD⊥AB于D,
∵AC=4cm,BC=3cm,AB=5cm,
又∵32+42=52,
∴△ACB是直角三角形,∠ACB=90°
由三角形的面积公式得:![]() ,
,
CD=2.4(cm),
由勾股定理得:AD=![]() =3.2(cm),BD=5cm﹣3.2cm=1.8cm,
=3.2(cm),BD=5cm﹣3.2cm=1.8cm,
绕着边AB旋转一周,所得的几何体的体积是:![]() ×π×2.42×3.2+
×π×2.42×3.2+![]() ×1.8=9.6π(cm)2.
×1.8=9.6π(cm)2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目