题目内容
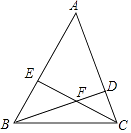
【题目】如图①，在△ABC中，∠ACB=90°，AC=BC= 
，D、E是AB边上的两个动点，满足∠DCE=45°． 
（1）如图②，把△ADC绕着点C顺时针旋转90°，得到△BKC，连结EK． 
①求证：△DCE≌△KCE．
②求证：DE2=AD2+BE2 ．
③思考与探究：当点D从点A向AB的中点运动的过程中，请尝试写出DE长度的变化趋势 
；并直接写出DE长度的最大值或最小值 （标明最大值或最小值）．
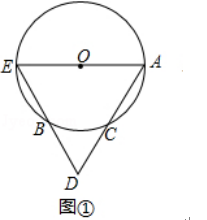
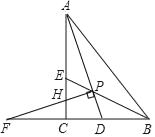
（2）如图③，若△CDE的外接圆⊙O分别交AC，BC于点F、G，求证：CF：CG=BE：AD． 
【答案】
（1）证明：①如图1，由旋转得：△ACD≌△BCK，
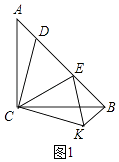
∴CD=CK，∠ACD=∠BCK，
∵∠DCE=45°，∠ACB=90°，
∴∠ACD+∠BCE=90°﹣45°=45°，
∴∠BCK+∠BCE=45°，
即∠KCE=45°，
∴∠KCE=∠DCE，
∵CE=CE，
∴△DCE≌△KCE（SAS）；
②如图2，∵△ABC是等腰直角三角形，
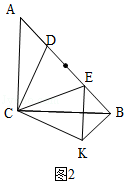
∴∠A=∠ABC=45°，
∵△DCE≌△KCE，
∴DE=EK，∠KBC=∠A=45°，KB=AD，
∴∠KBE=45°+45°=90°，
在Rt△KBE中，KE2=BE2+KB2，
∴DE2=AD2+BE2；|当D从A到D时，DE越来越小，再继续运动到中点时，越来越大；|DE最大值=1，DE最小值=2 
﹣2
③∵∠ACB=90°，AC=BC= ，
∴AB= 
=2，
设AD=x，DE=y，则BE=2﹣x﹣y，
当点D从点A向AB的中点运动的过程中，0≤y≤1，0≤x≤1，AD=BE时，DE最小，如图2，BE=BK=x，
则x=2﹣x﹣y，
y=2﹣2x，
∵KE2=BE2+KB2，
∴y2=x2+x2，
（2﹣2x）2=2x2，
x2﹣4x+2=0，
解得：x1=2+ （不符合题意，舍去），x2=2﹣ ，
∴y=2﹣2（2﹣ ）=2 ﹣2，
即DE的最小值是：2 ﹣2，
当D与A重合或D与AB的中点重合时，DE最大，最大值是1；
∴DE长度的变化趋势是：当D从A到D时，DE越来越小，再继续运动到中点时，越来越大；
故答案为：当D从A到D时，DE越来越小，再继续运动到中点时，越来越大；DE最大值=1， 
；
（2）如图3，把△ADC绕着点C顺时针旋转90°，得到△BKC，连结EK，EG，
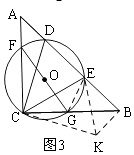
∵D、C、E、G四点共圆，
∴∠EGB=∠CDE，
∵∠DCE=∠EBC=45°，
在△CDE和△GEB中，∴∠CED=∠GEB，
由①得：△CDE≌△CKE，
∴∠CED=∠CEK，
∴∠CEK=∠GEB，
∴∠CEK﹣∠GEK=∠GEB﹣∠GEK，
即∠CEG=∠KEB，
∵∠CEG=∠CFG，
∴∠CFG=∠KEB，
∵∠ACB=∠EBK=90°，
∴△FCG∽△EBK，
∴ 
，
由①得：△ACD≌△BCK，
∴AD=BK，
∴CF：CG=BE：AD．
【解析】（1）①由旋转得：CD=CK，∠ACD=∠BCK，证明∠KCE=∠DCE=45°，根据SAS证明：△DCE≌△KCE；②先求∠KBE=45°+45°=90°，在Rt△KBE中，利用勾股定理可得结论；③如图2，本题可以看作是周长一定，即直角△EBK的周长为2，斜边DE的变化趋势，发现根据直角三角形斜边中线等于斜边的一半可知：DE的大小取决于直角△EBK斜边中线的大小，当直角△EBK是等腰直角三角形（设两直角边分别为a、b时，斜边为 
，因为a2+b2≥2ab，当a=b时， 有最小值）时，中线最短，由此计算DE的最小值，当D与A重合或D与AB的中点重合时，DE最大，最大值是1；（2）如图3，同①作辅助线，证明△FCG∽△EBK，列比例式得 ，由①得：△ACD≌△BCK， AD=BK，所以CF：CG=BE：AD．
