题目内容
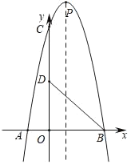
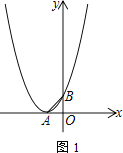
【题目】已知抛物线顶点![]() 在
在![]() 轴负半轴上,与
轴负半轴上,与![]() 轴交于点
轴交于点![]() ,
,![]() ,
,![]() 为等腰直角三角形.
为等腰直角三角形.
(1)求抛物线的解析式
(2)若点![]() 在抛物线上,若
在抛物线上,若![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标
的坐标
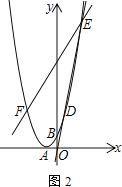
(3)已知直线![]() 过点
过点![]() ,交抛物线于点
,交抛物线于点![]() 、
、![]() ,过
,过![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,求证:直线
,求证:直线![]() 经过一个定点,并求定点的坐标.
经过一个定点,并求定点的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)(-1,4)
;(3)(-1,4)
【解析】
(1)先求出顶点坐标与y轴交点坐标,根据顶点式求二次函数解析式;
(2)根据直角三角形的判定定理找出△ABC为直角三角形,分三种情况:当A为直角顶点时,AC⊥AB;当B为直角顶点时,BC⊥AB;当C为直角顶点,分别确定点C的坐标;
(3)根据二次函数与方程的关系求解.
(1)∵OB=1,点B在y轴的正半轴上,
∴B(0,1),
∵△OAB为等腰直角三角形,
∴OA=OB=1,
∵顶点A在x轴负半轴上,
∴顶点A(-1,0),
∴设y=a(x+1)2,
把B(0,1)代入得
1=a×(0+1)2,
∴a=1,
∴![]() ,
,
(2)当A为直角顶点时,AC⊥AB,
设直线AB解析式为y=mx+n,
∵B(0,1),A(-1,0),
∴![]() ,
,
∴![]() ,
,
∴直线AB解析式为y=x+1,
∵AC⊥AB,
∴直线AC解析式为y=-x-1,
联立得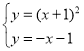 ,
,
解得: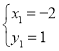 ,
,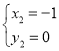 ,
,
∴C(-2,1).
当B为直角顶点时,BC⊥AB,
∵直线AB解析式为y=x+1,
∴直线BC解析式为y=-x+1,
同理可得C(-3,4),
当C为直角顶点不存在 .
综上所述点C坐标为(-2,1)或(-3,4),
(3)设DE的解析式为![]() ,
,
联立![]() ,
,
∴![]() ,
,
得: ,
,
∵D,E关于对称轴对称,
所以![]() ,
,
设EF的解析式为![]() 联立,
联立,
![]() ,
,
得![]() ,
,
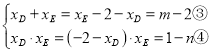 ,
,
联立①②③④得n=m+4,
所以![]() ,过定点(-1,4),
,过定点(-1,4),
即直线EF经过一个定点,定点的坐标为(-1,4).

 阅读快车系列答案
阅读快车系列答案【题目】某商店经过市场调查,整理出某种商品在第x(x≤90)天的售价与销量的相关信息如右表.已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元件) | x+40 | 90 |
每天销量(件) | 200-2x | |
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?