题目内容
【题目】阅读材料:
我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物;比如我们通过学习特殊的四边形,即平行四边形(继续学习它们的特殊类型如矩形、菱形等)来逐步认识四边形;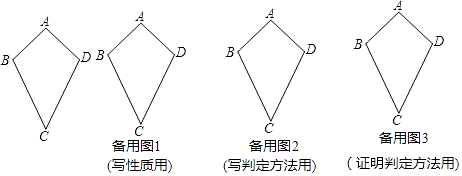
我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识;
请解决以下问题:
如图,我们把满足AB=AD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”;
(1)写出筝形的两个性质(定义除外);
(2)写出筝形的两个判定方法(定义除外),并选出一个进行证明.
【答案】
(1)解:性质1:只有一组对角相等(或者∠B=∠D,∠A≠∠C);
性质2:只有一条对角线平分对角;
也可参考:
性质3:两条对角线互相垂直,其中只有一条被另一条平分;
性质4:两组对边都不平行;
(2)解:判定方法1:只有一条对角线平分对角的四边形是筝形;
判定方法2:两条对角线互相垂直且只有一条被平分的四边形是筝形;
判定方法有如下参考选项:
判定方法3:AC⊥BD,∠B=∠D,∠A≠∠C;
判定方法4:AB=CD,∠B=∠D,∠A≠∠C;
判定方法5:AC⊥BD,AB=CD,∠A≠∠C.
判定方法1的证明:
已知:在四边形ABCD中,对角线AC平分∠A和∠C,对角线BD不平分∠B和∠D.
求证:四边形ABCD是筝形.
证明:∵∠BAC=∠DAC,∠BCA=∠DCA,AC=AC,
∴△ABC≌△ADC.
∴AB=CD,CB=CD,①
易知AC⊥BD.
又∵∠ABD≠∠CBD,
∴∠BAC≠∠BCA,∴AB≠BC.②
由①、②知四边形ABCD是筝形.
【解析】这是一道开放性的命题,(1)由条件可判定AC为BD的垂直平分线,则可得出相关性质;
(2)这题是文字证明题,先要根据命题写出已知求证,然后利用三角形全等得出相关的性质。
【考点精析】本题主要考查了线段垂直平分线的判定和线段垂直平分线的性质的相关知识点,需要掌握和一条线段两个端点距离相等的点,在这条线段的垂直平分线上;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等才能正确解答此题.

【题目】探索与应用.先填写下表,通过观察后再回答问题:
a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| … | 0.01 | x | 1 | y | 100 | … |
(1)表格中x= ;y= ;
(2)从表格中探究a与![]() 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知![]() ≈3.16,则
≈3.16,则![]() ≈ ;②已知
≈ ;②已知![]() =1.8,若
=1.8,若![]() =180,则a= ;
=180,则a= ;
(3)拓展:已知![]() ,若
,若![]() ,则b= .
,则b= .