题目内容
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t(s).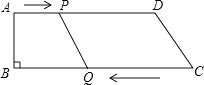
(1)当t为何值时,PQ∥CD?
(2)当t为何值时,PQ=CD?
【答案】
(1)解:根据题意得:PA=t,CQ=3t,则PD=AD﹣PA=24﹣t.
∵AD∥BC,
即PD∥CQ,
∴当PD=CQ时,四边形PQCD为平行四边形,
即24﹣t=3t,
解得:t=6,
即当t=6时,PQ∥CD;
(2)解:若PQ=DC,分两种情况:
①PD=QC,由(1)可知,t=6,
②PD≠CQ,则四边形PDCQ是等腰梯形,则有QC=PD+2(BC﹣AD),
可得方程:3t=24﹣t+4,
解得:t=7.
【解析】(1)根据题意得:PA=t,CQ=3t,则PD=AD﹣PA=24﹣t.根据一组对边平行且相等得四边形是平行四边形得出方程,求解得出t的值,然后根据平行四边形的性质定理得出结论;
(2)若PQ=DC,分两种情况:①PQ=DC,由(1)可知,t=6,②PD≠CQ,则四边形PDCQ是等腰梯形,则有QC=PD+2(BC﹣AD),得出方程求解即可。
【考点精析】关于本题考查的平行四边形的判定与性质和直角梯形,需要了解若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;一腰垂直于底的梯形是直角梯形才能得出正确答案.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目