题目内容
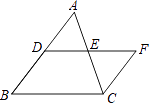
【题目】如图,在□ABCD中,E是AD的中点,连接BE并延长BE交CD的延长线于点F。
(1)求证:△ABE≌△DFE。
(2)连接BD,AF,当BE平分∠ABD时,求证:四边形ABDF是菱形。
【答案】(1)证明见解析;(2)证明见解析
【解析】证明:(1)∵四边形ABCD为平行四边形 ∴AB∥CD
∵点F在CD的延长线上 ∴FD∥AB
∴∠ABE = ∠DFE
∵E是AB的中点 ∴AE = DE
在△ABE和△DFE中
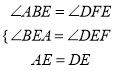
∴△ABE≌△DFE
(2)∵△ABE≌△DFE
∴AB=DF
∵AB∥DF,AB=DF
∴四边形ABDF是平行四边形
∵BF平分∠ABD
∴∠ABF=∠DBF
∵AB∥DF
∴∠ABF=∠DFB
∴∠DBF=∠DFB
∴DB=DF
∴四边形ABDF是菱形。

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
【题目】某鞋店对上一周某品牌女鞋的销量统计如下:
尺码(厘米) | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
销量(双) | 1 | 2 | 5 | 11 | 7 | 3 | 1 |
该店决定本周进货时,多进一些尺码为23.5厘米的鞋,影响鞋店决策的统计量是:( )
A. 平均数B. 中位数C. 方差D. 众数