Question

【题目】五边形ABCDE中，∠EAB=∠ABC=∠BCD=90°，AB=BC，且满足以点B为圆心，AB长为半径的圆弧AC与边DE相切于点F，连接BE，BD．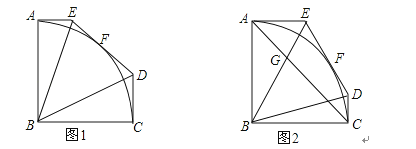

（1）如图1，求∠EBD的度数;
（2）如图2，连接AC，分别与BE，BD相交于点G，H，若AB=1，∠DBC=15°，求AGHC的值．

Answer 1

【答案】
（1）

【解答】解：如图1，

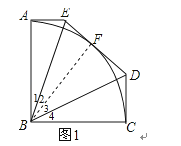
连接BF，

∵DE与⊙B相切于点F，

∴BF⊥DE，

在Rt△BAE与Rt△BEF中，

，

∴Rt△BAE≌Rt△BEF，

∴∠1=∠2，

同理∠3=∠4，

∵∠ABC=90°，

∴∠2+∠3=45°，

即∠EBD=45°；

（2）

【解答】

如图2，

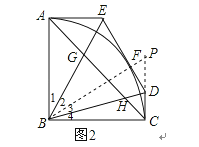
连接BF并延长交CD的延长线于P，

∵∠4=15°，

由（1）知，∠3=∠4=15°，

∴∠1=∠2=30°，∠PBC=30°，

∵∠EAB=∠PCB=90°，AB=1，

∴AE=，BE=，

在△ABE与△PBC中，，

∴△ABE≌△PBC，

∴PB=BE=，

∴PF=-1，

∵∠P=60°，

∴DF=2﹣，

∴CD=DF=2﹣，

∵∠EAG=∠DCH=45°，

∠AGE=∠BDC=75°，

∴△AEG∽△CHD，

∴，

∴AGCH=CDAE，

∴AGCH=CDAE=（2﹣）=．

【解析】（1）如图1，连接BF，由DE与⊙B相切于点F，得到BF⊥DE，通过Rt△BAE≌Rt△BEF，得到∠1=∠2，同理∠3=∠4，于是结论可得；
（2）如图2，连接BF并延长交CD的延长线于P，由△ABE≌△PBC，得到PB=BE=，求出PF=-1，通过△AEG∽△CHD，列比例式即可得到结果．
【考点精析】通过灵活运用切线的性质定理和相似三角形的判定与性质，掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方即可以解答此题．