题目内容
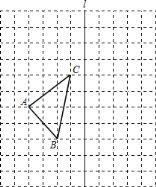
【题目】 如图,在11×11的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求A与A1,B与B1,C与C1相对应)
(2)作出△ABC绕点C顺时针方向旋转90°后得到的△A2B2C2;
(3)在(2)的条件下求出线段AC在旋转中所扫过的面积.(结果保留π)
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)利用轴对称的性质分别画出A、B、C关于直线l的对称点A1、B1、C1即可;
(2)利用网格特点和旋转的性质画出A、B、C的对应点A2、B2、C2即可;
(3)根据扇形的面积公式![]() 计算即可.
计算即可.
解:(1)如图,△A1B1C1即为所求三角形;

(2)如图,△A2B2C2即为所求三角形;
(3)由题意及图形可知,∠ACA2=90°,AC=![]() =
=![]() ,
,
∴线段AC在旋转中所扫过的面积=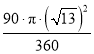 =
=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某商场计划销售某种产品,现邀请生产该产品的甲、乙两个厂家进场试销10天.两个厂家提供的返利方案如下:甲厂家每天固定返利70元,且每卖出一件产品厂家再返利2元;乙厂家无固定返利,卖出40件以内(含40件)的产品,每件产品厂家返利4元,超出40件的部分每件返利6元.两个厂家销售情况如下表:
甲厂家销量(件) | 38 | 39 | 40 | 41 | 42 |
天数 | 2 | 4 | 2 | 1 | 1 |
乙厂家销量(件) | 38 | 39 | 40 | 41 | 42 |
天数 | 1 | 2 | 2 | 4 | 1 |
(1)现从乙厂家试销的10天中随机抽取1天,求这1天的返利不超过160元的概率;
(2)商场拟甲、乙两个厂家中选择一个长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场作出选择,并说明理由.