题目内容
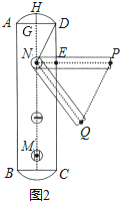
【题目】在等边![]() 中,
中,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 上任意一点,连接
上任意一点,连接![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上一点,且
上一点,且![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
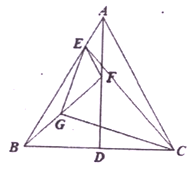
(1)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)求证:![]() .
.
【答案】(1)![]() (2)证明见详解
(2)证明见详解
【解析】
(1)根据等边三角形性质可知BD=![]() BC=
BC=![]() ,利用勾股定理求出AD的长,再利用勾股定理求出BF的值;
,利用勾股定理求出AD的长,再利用勾股定理求出BF的值;
(2)先延长EG至H,使GH=EG,连接BH、CH、FH,构造全等三角形,证四边形BHFE是平行四边形,推出BH∥EF,再由AE=EF,推出AC∥EF,得出AC∥BH,根据平行线的性质推出∠ACB=∠CBH=60°,根据三角形全等的判定和性质得出△CEH是等边三角形,再根据等边三角形性质求得结论即可.
(1)解:∵在等边![]() 中,
中,![]() 于点
于点![]() ,
,![]()
∴AC=BC=AB=![]() ,BD=
,BD=![]() BC=
BC=![]()
∴AD=![]()
∵![]()
∴DF=15-6=9
∴BF=![]()
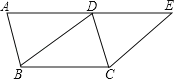
(2)证明:延长EG至H,使GH=EG,连接BH、CH、FH,
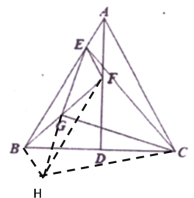
∵点![]() 为
为![]() 的中点,∴BG=FG
的中点,∴BG=FG
∴四边形BHFE是平行四边形,
∴BH=EF,BH∥EF
∵AE=EF ∴BH=AE,∠EAF=∠EFA=∠DAC
∴AC∥EF ∴AC∥BH
∴∠ACB=∠CBH=60°
在△AEC和△BHC中
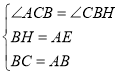
∴△AEC≌△BHC(SAS)
∴∠ACE=∠BCH EC=HC
∴∠ECB+∠ACE=∠ECB+∠BCH=60°即∠ECH=60°
∴△CEH是等边三角形,GH=EG,
∴∠CGE=90°,∠ECG=30°
∴tan30°=EG∶CG=1∶![]()
∴CG=![]() EG
EG

【题目】某保健品厂每天生产A,B两种品牌的保健品共600瓶,A,B两种产品每瓶的成本和售价如下表,设每天生产A产品x瓶,生产这两种产品每天共获利y元.
A | B | |
成本(元)/瓶 | 50 | 35 |
售价(元)/瓶 | 70 | 50 |
(1)请求出y关于x的函数关系;
(2)该厂每天生产的A,B两种产品被某经销商全部订购,厂家对B产品不变,对A产品进行让利,每瓶利润降低![]() 元,厂家如何生产可使每天获利最大?最大利润是多少?
元,厂家如何生产可使每天获利最大?最大利润是多少?