��Ŀ����
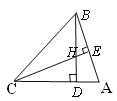
����Ŀ����֪������ABC�У���BAC=90������ABC=45������DΪֱ��BC��һ���㣨��D�����B��C�غϣ�����ADΪ����������ADEF������CF��
��1����ͼ��������D���߶�BC��ʱ����֤��CF+CD=BC��
��2����ͼ��������D���߶�BC���ӳ�����ʱ�������������䣬��ֱ��д��CF��BC��CD�����߶�֮��Ĺ�ϵ��
��3����ͼ��������D���߶�BC�ķ����ӳ�����ʱ���ҵ�A��F�ֱ���ֱ��BC�����࣬�����������䣻
����ֱ��д��CF��BC��CD�����߶�֮��Ĺ�ϵ��
����������ADEF�ı߳�Ϊ![]() ���Խ���AE��DF�ཻ�ڵ�O������OC����OC�ij�����
���Խ���AE��DF�ཻ�ڵ�O������OC����OC�ij�����
���𰸡�(1)��֤�����̼�������(2)��CF��CD=BC��(3)��CD��CF=BC��2.
��������
���������(1)�����������ε������ж�����BAD����CAFȫ�ȣ��Ӷ��ó�BD=CF������BD+CD=BC�ó��𰸣�(2)������ͼ�εó��߶�֮��Ĺ�ϵ��(3)�����ȸ��������ε�����֤����BAD����CAFȫ�ȣ�Ȼ��ó���ACF=��ABD=135�����Ӷ�˵����FCDΪֱ�������Σ����������εĶԽ��ߵó�DF�ij��ȣ�Ȼ�����ֱ��������б���ϵ����ߵ����ʵó�OC�ij���.
���������(1)���ߡ�BAC=90������ABC=45�������ACB=��ABC=45������AB=AC��
���ı���ADEF�������Σ���AD=AF����DAF=90����
�ߡ�BAD=90��-��DAC����CAF=90��-��DAC�����BAD=��CAF��
������BAD����CAF�� ���BAD �� ��CAF��SAS������BD=CF��
���BAD �� ��CAF��SAS������BD=CF��
��BD+CD=BC����CF+CD=BC��
(2)��CF��CD=BC
(3)����CD��CF =BC��
�ڡߡ�BAC=90������ABC=45�������ACB=��ABC=45������AB=AC�� ���ı���ADEF�������Σ�
��AD=AF����DAF=90���� �ߡ�BAD=90��-��BAF����CAF=90��-��BAF�����BAD=��CAF��
������BAD����CAF�� ���BAD �� ��CAF��SAS����
���BAD �� ��CAF��SAS����
���ABD=��ACF���ߡ�ABC=45������ABD=135���� ���ACF=��ABD=135����
���FCD=90�������FCD��ֱ�������Σ� ��������ADEF�ı߳�Ϊ![]() �ҶԽ���AE��DF�ཻ�ڵ�O��
�ҶԽ���AE��DF�ཻ�ڵ�O��
��DF=![]() AD=4��OΪDF�е㣮 ��OC=
AD=4��OΪDF�е㣮 ��OC=![]() DF=2��
DF=2��