Question

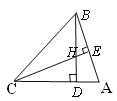
【题目】如图，在△ABC中，∠A︰∠B︰∠C=5︰4︰3，BD、CE分别是边AC、AB上的高，BD、CE相交于点H，求∠BHC的度数.

Answer 1

【答案】105°

【解析】试题分析：本题先根据三角形内角和定理，求出△ABC三个内角的度数；然后利用垂直定义及四边形AEHD的内角和等于360°，求出∠EHD的度数，即∠BHC的度数．

试题解析：解：在△ABC中，∵∠A=5x°，∠ABC=4x°，∠ACB=3x°．

又∵∠A+∠ABC+∠ACB=180°，∴5x°+4x°+3x°=180°，解得x=15，∠A=5x°=75°，∵BD，CE分别是边AC，AB上的高，∴∠ADB=90°，∠BEC=90°，∵在四边形AEHD中，∠DHE=360°﹣∠ADB﹣∠AEC﹣∠A=360°﹣90°﹣90°﹣75°=105°，∴∠BHC=∠DHE =105°．