Question

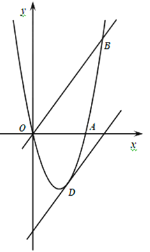
【题目】如图，已知抛物线与x轴交于点和点，与轴交于点.

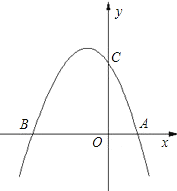
（1）求抛物线的解析式；
（2）若点为第二象限抛物线上一动点，连接，求面积的最大值，并求此时点的坐标．
（3）在抛物线上是否存在点使得为等腰三角形？若存在，请求出一共有几个符合条件的点（简要说明理由）并写出其中一个点的坐标；若不存在这样的点，请简要说明理由．

Answer 1

【答案】（1）y=-x2-2x+3；（2）点E的坐标为（-，）；（3）存在．共有5个点，其中一个是（-1，4）．

【解析】

（1）由抛物线y=ax2+bx+3（a≠0）与x轴交于点A（1，0）和点B（-3，0），利用待定系数法，将点A与B的坐标代入抛物线的解析式即可求得a与b的值，则可得此抛物线的解析式；
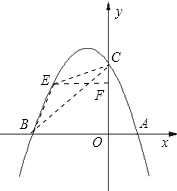
（2）根据已知可求得点C的坐标，然后作辅助线：EF∥AB，设点E的坐标为（x，y），由S△BEC=S梯形OBEF+S△EFC-S△BOC即可求得关于x的二次函数，配方即可求得x的值，代入解析式，求得y的值；
（3）分别从AP=BP与AB=BP与AB=AP去分析，可得到存在符合条件的点有5个，其中最好求的是P在顶点时的坐标，配方求解即可．

（1）将点A与B的坐标代入抛物线的解析式得： ，
解得：，
∴抛物线的解析式为：y=-x2-2x+3；

（2）∵抛物线的解析式为：y=-x2-2x+3，
∴点C的坐标为（0，3），
设点E的坐标为（x，y），过点E作EF∥AB交y轴于F，
∴EF=-x，OB=3，OC=3，OF=-x2-2x+3，CF=3-（-x2-2x+3）=x2+2x，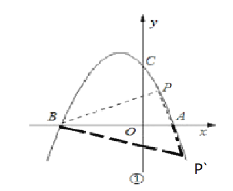

∴S△BEC=S梯形OBEF+S△EFC-S△BOC
=（EF+OB）OF+EFCF-OBOC
=×（-x+3）×（-x2-2x+3）+×（-x）×（x2+2x）-×3×3
=-（x+）2+，
∴当x=-时，△BCE的面积最大，最大面积为；
∴y=-x2-2x+3=，
∴点E的坐标为（-，）；

（3）存在．
如果AP=BP，则点P在AB的垂直平分线上，即是抛物线的顶点，
∵y=-x2-2x+3=-（x+1）2+4，
∴此时P点的坐标为（-1，4）；
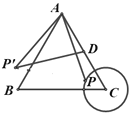
如果AB=BP，则如图①：
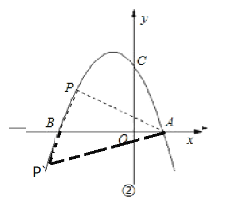
如果AB=AP，则如图②：
∴存在使得△ABP为等腰三角形的P点5个；
有一点的坐标为（-1，4）．