题目内容
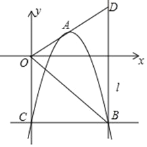
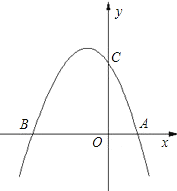
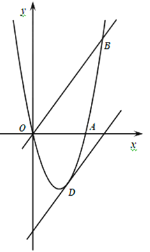
【题目】如图:已知抛物线y=ax2+bx(a≠0)经过A(3,0),B(4,4)两点.
(1)求抛物线解析式.
(2)将直线OB向下平移m个单位后,得到的直线与抛物线只有一个公共点D,求m值及交点D的坐标.
【答案】(1) y=x2-3x ;(2)m=4,D(2,-2).
【解析】
(1)利用待定系数法求出二次函数解析式即可;
(2)根据已知条件可求出OB的解析式为y=x,则向下平移m个单位长度后的解析式为:y=xm.由于抛物线与直线只有一个公共点,意味着联立解析式后得到的一元二次方程,其根的判别式等于0,由此可求出m的值和D点坐标.
(1)∵抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)
∴将A与B两点坐标代入得:
![]() ,
,
解得:![]() ,
,
∴抛物线的解析式是y=x23x.
(2)设直线OB的解析式为y=k1x,由点B(4,4),
得:4=4k1,解得:k1=1
∴直线OB的解析式为y=x,
∴直线OB向下平移m个单位长度后的解析式为:y=xm,
∵点D在抛物线y=x23x上,
∴可设D(x,x23x),
又∵点D在直线y=xm上,
∴x23x=xm,即x24x+m=0,
∵抛物线与直线只有一个公共点,
∴△=164m=0,
解得:m=4,
此时x1=x2=2,y=x23x=2,
∴D点的坐标为(2,2).

练习册系列答案
相关题目
【题目】某农科所在相同条件下做某种作物种子发芽率的试验,结果如表所示:
种子个数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
发芽种子个数m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
发芽种子频率 | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
则该作物种子发芽的概率约为_____________.(保留一位小数)