Question

【题目】如图，在△ABC中，∠ACB＝α，将△ABC绕点C顺时针方向旋转到△A′B′C的位置，使AA′∥BC，设旋转角为β，则α，β满足关系（　　）

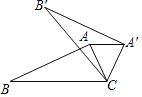
A.α+β＝90°B.α+2β＝180°C.2α+β＝180°D.α+β＝180°

Answer 1

【答案】C

【解析】

由旋转的性质和平行线的性质得到∠CAA′=∠ACB=α，AC=A′C，根据等腰三角形的性质得到∠AA′C=∠A′AC=α；根据三角形的内角和即可得到即可．

解：当△ABC绕点C顺时针旋转到△A′B′C的位置，使AA′∥BC，

∴∠CAA′＝∠ACB＝α，AC＝A′C，

∴∠AA′C＝∠A′AC＝α；

∴∠ACA′＝180°﹣∠CAA′﹣∠CA′A＝180°﹣2α＝β，

∴2α+β＝180°，

故选：C．