��Ŀ����
����Ŀ���Ķ�������ϣ�
��A��B�������Ϸֱ��ʾʵ��a��b��A��B����֮��ľ����ʾΪ|AB|
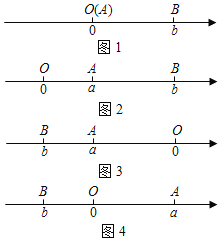
��A��B��������һ����ԭ��ʱ���������A��ԭ�㣨��ͼ1��|AB|��|OB|��|b|��|a��b|��
��A��B���㶼����ԭ��ʱ
�ٵ���A��B����ԭ����ұߣ���ͼ2��
|AB|��|OB|��|OA|��|b|��|a|��b��a��|a��b|
�ڵ���A��B����ԭ�����ߣ���ͼ3��
|AB|��|OB|��|OA|��|b|��|a|����b������a����|a��b|
�۵���A��B��ԭ������ߣ���ͼ4��
|AB|��|OB|+|OA|��|b|+|a|����b+a��|a��b|
�ش��������⣺
��1�������ϱ�ʾ1��5������֮��ľ������� ���������ϱ�ʾ1�ͩ�3������֮��ľ������� ����
��2������������A��ʾ������x����B��ʾ�����ǩ�2�����A��B֮��ľ������� ������|AB|��3����ôxΪ�� ����
��3����x���� ��ʱ������ʽ|x+2|+|x��1|��5��
��4������A��ʾ������1����B���A�ľ�����10���ҵ�B�ڵ�A���Ҳ࣬����P��Qͬʱ��A��B�����������������˶�����P���ٶ���ÿ��3����λ���ȣ���Q���ٶ���ÿ��![]() ����λ���ȣ����˶������Q���P���1����λ������д����Ҫ�������̣�
����λ���ȣ����˶������Q���P���1����λ������д����Ҫ�������̣�
���𰸡���1��4��4����2��|x+2|����5��1����3����3��2����4���˶�![]() ��
��![]() ���P���Q֮��ľ���Ϊ1��λ����
���P���Q֮��ľ���Ϊ1��λ����
��������
��1�����������ľ��빫ʽ������⣻
��2�����������ľ��빫ʽ���������ϱ�ʾx�ͩ�2������A��B֮��ľ��룬�ٸ��������ľ��빫ʽ�г����̿���x��
��3��������������ۣ��ٵ�x����2ʱ���ڵ���2��x��1ʱ���۵�x��1ʱ���ֱ���м�����ֵ���ɣ�
��4������PQ�ľ���Ϊ1�г����̣��ⷽ�̣��ɵô𰸣�
�⣺��1�������ϱ�ʾ1��5����֮��ľ����ǣ�|1��5|��4��
�����ϱ�ʾ1�ͩ�3������֮��ľ����ǣ�|��3��1|��4��
�ʴ�Ϊ��4��4��
��2�������ϱ�ʾx�ͩ�2������A��B֮��ľ����ǣ�|x+2|��
��|AB|��3����|x+2|��3��
���x����5��1��
�ʴ�Ϊ��|x+2|����5��1��
��3����|x+2|+|x��1|��5��
��ٵ�x����2ʱ����x��2��x+1��5�����x����3��
�ڵ���2��x��1ʱ��x+2��x+1��5���˷����⣻
�۵�x��1ʱ��x+2+x��1��5�����x��2��
�ʴ�Ϊ����3��2��
��4�����˶�x���Q���P ���1����λ�������⣬��
��P����Q����1+3x����9+![]() x����1��
x����1��
���x��![]() ��
��
��P��Q�ĺ�ߣ�9+![]() x������1+3x����1��
x������1+3x����1��
���x��![]() ��
��
���˶�![]() ��
��![]() ���P���Q֮��ľ���Ϊ1��λ���ȣ�
���P���Q֮��ľ���Ϊ1��λ���ȣ�