题目内容
【题目】已知圆内一点到圆周上的点的最大距离是7，最小距离是5，则该圆的半径是__________.
【答案】6
【解析】由题意，得
该圆的半径为： 
. 理由如下.
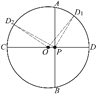
如图，设圆心为点O，该圆内的点为点P，过点P作直径CD，过点P作弦AB⊥CD.
不妨在圆周上任意取异于点D与点C的两点D1，D2. 连接OD1，OD2，PD1，PD2.
设该圆的半径为r，则OD=OC=OD1=OD2=r.
点P到点D的距离PD=OD-OP=r-OP，点P到点C的距离PC=OC+OP=r+OP.
∴PC>PD.
在△OPD1中，PD1>OD1-OP=r-OP=PD；在△OPD2中，PD2>OD2-OP=r-OP=PD.
∴PD1>PD，PD2>PD，PC>PD.
∴点P到点D的距离PD是点P与圆周上的点的最小距离.
在△OPD1中，PD1<OD1+OP=r+OP=PC；在△OPD2中，PD2<OD2+OP=r+OP=PC.
∴PD1<PC，PD2<PC，PD<PC.
∴点P到点C的距离PC是点P与圆周上的点的最大距离.
综上所述，对于圆内的一点，它到圆周上的点的最大距离与最小距离之和恰好等于圆的直径，故该圆的半径为上述最大距离与最小距离之和的一半.
故本题应填写：6.
练习册系列答案
百分学生作业本题练王系列答案
互动课堂系列答案
相关题目
