题目内容
【题目】请认真观察图形,解答下列问题:
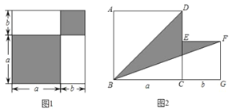
(1)根据图1中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法1: .
方法2: .
(2)从中你能发现什么结论?请用等式表示出来: .
(3)利用(2)中结论解决下面的问题:如图2,两个正方形边长分别为a、b,如果a+b=10,ab=21,求阴影部分的面积.
【答案】(1)方法1:a2+b2 ;方法2:(a+b)2﹣2ab;(2)a2+b2=(a+b)2﹣2ab;(3)阴影部分的面积=18.5.
【解析】
(1)方法1:两个正方形面积和,方法2:大正方形面积-两个小长方形面积;
(2)由题意结合(1)的结果可直接得到;
(3)由阴影部分面积=正方形ABCD的面积+正方形CGFE的面积-三角形ABD的面积-三角形BGF的面积,可求阴影部分的面积.
(1)由题意可得:方法1:a2+b2 ,
方法2:(a+b)2﹣2ab;
(2)a2+b2=(a+b)2﹣2ab;
(3)∵阴影部分的面积=S正方形ABCD+S正方形CGFE﹣S△ABD﹣S△BGF
=a2+b2﹣![]() a2﹣
a2﹣![]() (a+b)b,
(a+b)b,
∴阴影部分的面积=![]() a2+
a2+![]() b2﹣
b2﹣![]() ab=
ab=![]() [(a+b)2﹣2ab]﹣
[(a+b)2﹣2ab]﹣![]() ab=18.5.
ab=18.5.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目