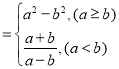题目内容
【题目】如图,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 与
与![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)求抛物线的解析式;
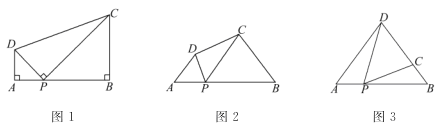
(2)如图1,点![]() 是抛物线上(
是抛物线上(![]() 轴下方)的一个动点,过点
轴下方)的一个动点,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() 试判断在点
试判断在点![]() 运动过程中,以点
运动过程中,以点![]() 为顶点的四边形能否构成平行四边形,若能,请求出点
为顶点的四边形能否构成平行四边形,若能,请求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
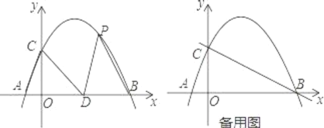
(3)如图2,点![]() 是抛物线的顶点,抛物线的对称轴
是抛物线的顶点,抛物线的对称轴![]() 交
交![]() 轴于点
轴于点![]() 当点
当点![]() 在抛物线上
在抛物线上![]() 之间运动时,连接
之间运动时,连接![]() 交
交![]() 于点
于点![]() 连接
连接![]() 并延长交
并延长交![]() 于点
于点![]() 猜想在点
猜想在点![]() 的运动过程中,
的运动过程中,![]() 的和是否为定值?若是,试求出该定值;若不是,请说明理由.
的和是否为定值?若是,试求出该定值;若不是,请说明理由.

【答案】(1)![]() ;(2)能,点
;(2)能,点![]() 的坐标为
的坐标为![]() 或
或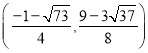 ;(3)
;(3)![]() 的和是定值,该定值为
的和是定值,该定值为![]() .
.
【解析】
(1)设抛物线的解析式为![]() ,把点
,把点![]() 代入,得
代入,得![]() 即可求出解析式;
即可求出解析式;
(2)设点![]() 求出直线
求出直线![]() ,再求EF的长,得到
,再求EF的长,得到![]() 解方程求出m的值,即可求出点
解方程求出m的值,即可求出点![]() 的坐标;
的坐标;
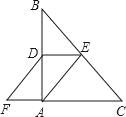
(3)作![]() 于点
于点![]() 证明
证明![]() 和
和![]() ,列出比例式,设点
,列出比例式,设点![]() 得出
得出![]() ,即可到答案.
,即可到答案.
解:![]() 抛物线
抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 与
与![]()
与直线![]() 交于点
交于点![]() ,
,
![]() 设抛物线的解析式为
设抛物线的解析式为![]()
把点![]() 代入,得
代入,得![]()
![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;
![]() 以点
以点![]() 为顶点的四边形构成平行四边形,
为顶点的四边形构成平行四边形,
设点![]()
![]() 直线
直线![]() 经过点
经过点![]() ,
,
即![]()
![]() 过点
过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]()
![]()
即![]() ,
,
![]()
![]()
解得![]() (舍去)或m=-
(舍去)或m=-![]() 或
或![]() 或
或![]() (舍去)
(舍去)
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或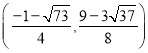
![]() 如图,作
如图,作![]() 于点
于点![]()
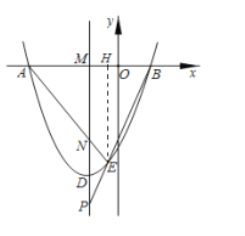
则![]()
![]() 即
即![]()
![]() 即
即![]()
设点![]() ,
,
则![]()
![]()
![]()
即![]()
![]() 在点
在点![]() 的运动过程中,
的运动过程中,![]() 的和是定值,该定值为
的和是定值,该定值为![]() .
.

练习册系列答案
相关题目
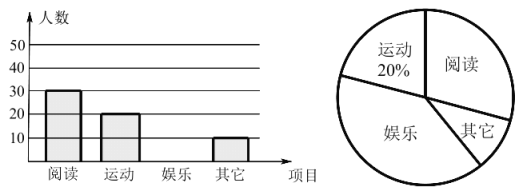
【题目】为响应市政府关于“垃圾不落地,市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的了解情况,对该校部分学生进行了问卷调查,并将调查结果分为![]() 四类(其中
四类(其中![]() 类表示“非常了解”,
类表示“非常了解”,![]() 类表示“比较了解”,
类表示“比较了解”,![]() 类表示“基本了解”,
类表示“基本了解”,![]() 类表示“不太了解”).根据调查结果得到如下不完整的统计表和统计图.请解答下列问题:
类表示“不太了解”).根据调查结果得到如下不完整的统计表和统计图.请解答下列问题:
了解程度 | 人数(人) | 所占百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
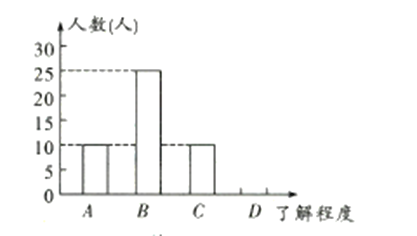
![]() ,
,![]() .
.
![]() 补全条形统计图;
补全条形统计图;
![]() 若该校共有学生
若该校共有学生![]() 人,估计该校对垃圾分类知识“非常了解”的有多少人?
人,估计该校对垃圾分类知识“非常了解”的有多少人?