题目内容
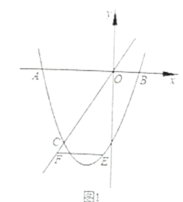
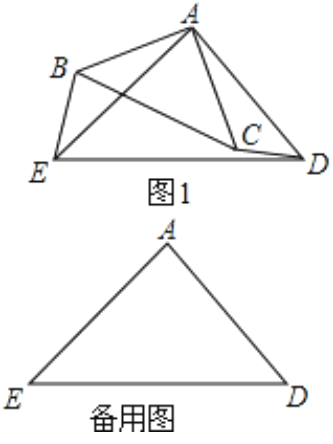
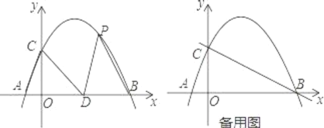
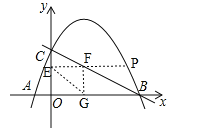
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过点A(﹣1,0)和点B(4,0),且与y轴交于点C,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点,连接CA,CD,PD,PB.
(1)求该抛物线的解析式;
(2)当△PDB的面积等于△CAD的面积时,求点P的坐标;
(3)当m>0,n>0时,过点P作直线PE⊥y轴于点E交直线BC于点F,过点F作FG⊥x轴于点G,连接EG,请直接写出随着点P的运动,线段EG的最小值.
【答案】(1)![]() ;(2)点P的坐标是(1,3)、(2,3)、(5,-3)或(-2,-3);(3)线段EG的最小值为
;(2)点P的坐标是(1,3)、(2,3)、(5,-3)或(-2,-3);(3)线段EG的最小值为![]() ..
..
【解析】
(1)根据抛物线y=ax2+bx+2经过点A(-1,0)和点B(4,0),应用待定系数法,求出该抛物线的解析式即可;
(2)首先根据三角形的面积的求法,求出△CAD的面积,即可求出△PDB的面积,然后求出BD=2,即可求出|n|=3,据此判断出n=3或-3,再把它代入抛物线的解析式,求出x的值是多少,即可判断出点P的坐标;
(3)首先应用待定系数法,求出BC所在的直线的解析式,然后根据点P的坐标是(m,n),求出点F的坐标,再根据二次函数最值的求法,求出EG2的最小值,即可求出线段EG的最小值.
解:(1)把A(-1,0),B(4,0)两点的坐标代入y=ax2+bx+2中,可得
![]() ,
,
解得: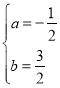 ,
,
∴抛物线的解析式为:![]() ;
;
(2))∵抛物线的解析式为![]() ,
,
当x=0时,y=2,
∴点C的坐标是(0,2),
∵点A(-1,0)、点D(2,0),
∴AD=2-(-1)=3,
∴S△CAD =![]() ,
,
∴S△PDB =3,
∵点B(4,0)、点D(2,0),
∴BD=2,
∴|n|=3×2÷2=3,
∴n=3或-3,
①当n=3时,
![]() ,
,
解得:m=1或m=2,
∴点P的坐标是(1,3)或(2,3);
②当n=-3时,
![]()
解得m=5或m=-2,
∴点P的坐标是(5,-3)或(-2,-3);
综上,可得点P的坐标是(1,3)、(2,3)、(5,-3)或(-2,-3);
(3)如图,
设BC所在的直线的解析式是:y=mx+n,
∵点C的坐标是(0,2),点B的坐标是(4,0),
∴![]() ,
,
解得: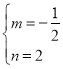 ,
,
∴BC所在的直线的解析式是:![]() ,
,
∵点P的坐标是(m,n),
∴点F的坐标是(4-2n,n),
∴![]()
![]()
![]() ,
,
∴当![]() 时,线段EG有最小值:
时,线段EG有最小值:![]() ,
,
∴线段EG的最小值为![]() .
.

【题目】已知水银体温计的读数y(℃)与水银柱的长度x(cm)之间是一次函数关系.现有一支水银体温计,其部分刻度线不清晰(如图),表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度.
水银柱的长度x(cm) | 4.2 | … | 8.2 | 9.8 |
体温计的读数y(℃) | 35.0 | … | 40.0 | 42.0 |
(1)求y关于x的函数关系式(不需要写出函数的定义域)
(2)用该体温计测体温时,水银柱的长度为6.6cm,求此时体温计的读数.
![]()