题目内容
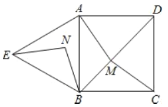
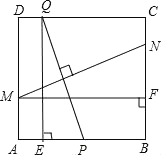
【题目】如图,在边长为2的正方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为边
为边![]() 上一动点,设
上一动点,设![]() ,线段
,线段![]() 的垂直平分线分别交边
的垂直平分线分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() .
.
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)顺次连接![]() 、
、![]() 、
、![]() 、
、![]() ,设四边形
,设四边形![]() 的面积为
的面积为![]() ,求出
,求出![]() 与自变量
与自变量![]() 之间的函数关系式,并求
之间的函数关系式,并求![]() 的最小值.
的最小值.
【答案】(1)见解析;(2)![]() ,
,![]() 的最小值为2
的最小值为2
【解析】
(1)由四边形![]() 是正方形得到
是正方形得到![]() ,
,![]() ,又由
,又由![]() ,利用ASA即可证得;
,利用ASA即可证得;
(2)分为两种情况:①当![]() 在
在![]() 上时,由点
上时,由点![]() 是边
是边![]() 的中点,
的中点,![]() ,
,![]() ,又由勾股定理求得
,又由勾股定理求得![]() ,由
,由![]() 得到
得到![]() 的值,又
的值,又![]() 求得面积
求得面积![]() ,由
,由![]() 范围得到
范围得到![]() 的最小值;②当
的最小值;②当![]() 在
在![]() 上时,同法可求
上时,同法可求![]() 的最小值.
的最小值.
解:(1)证明:∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 、
、![]() 都是矩形,
都是矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∴MF=QE
又∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
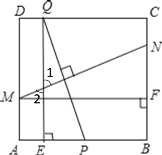
(2)解:分为两种情况:①当![]() 在
在![]() 上时,
上时,
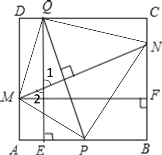
∵点![]() 是边
是边![]() 的中点,
的中点,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
由勾股定理,得![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵0≤AE≤AP
∴![]() ,
,
∴当![]() 时,
时,![]() .
.
②当![]() 在
在![]() 上时,
上时,
∵点![]() 是边
是边![]() 的中点,
的中点,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
由勾股定理,得![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵AP≤AE≤AB
∴![]() ,
,
∴当![]() 时,
时,![]() .
.
综上:![]() ,
,![]() 的最小值为2.
的最小值为2.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目