Question

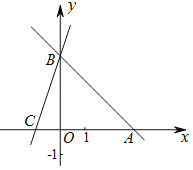
【题目】如图，直线y＝﹣x+b分别与x轴、y轴交于A，B两点，点A的坐标为（3，0），过点B的另一条直线交x轴负半轴于点C，且OB：OC＝3：1．

（1）求点B的坐标及直线BC对应的函数表达式；

（2）在线段OB上存在点P，使得点P到点B，C的距离相等，试求出点P的坐标；

（3）如果在x轴上方存在点D，使得以点A，B，D为顶点的三角形与△ABC全等，请直接写出点D的坐标．

Answer 1

【答案】（1）B（0，3），y＝3x+3；（2）P的坐标（0，）；（3）（4，3）或（3，4）．

【解析】

（1）先把A点坐标代入y=-x+b可计算出b=3，即可得到C点坐标，进而得出直线BC的解析式；

（2）设PB=PC=x，根据勾股定理解答即可;

（3）点A，B，D为顶点的三角形与△ABC全等，利用长度公式得出点D的坐标.

解：（1）把A （3，0）代入y＝﹣x+b，得 b＝3，

∴B（0，3），

∴OB＝3，

∵OB：OC＝3：1，

∴OC＝1，

∵点C在x轴负半轴上，

∴C（﹣1，0），

设直线BC的解析式为y＝mx+n，

把B（0，3）及C（﹣1，0）代入，得，

解得 ．

∴直线BC的解析式为：y＝3x+3；

（2）由题意，PB＝PC，

设PB＝PC＝x，则OP＝3﹣x，

在Rt△POC中，∠POC＝90°，

∴ ，

∴ ，

解得，x＝，

∴OP＝3﹣x＝，

∴点P的坐标（0，）；

（3）①如图，当点D在y轴右侧时，

点A，B，D为顶点的三角形与△ABC全等，则四边形BDAC为平行四边形，

则BD＝AC＝1+3＝4，则点D（4，3），

②当点D在y轴左侧时，

则S△ABD＝S△ABD′，则点D、D′到AB的距离相等，

则直线DD′∥AB，

设：直线DD′的表达式为：y＝﹣x+n，

将点D的坐标代入上式并解得：n＝7，

直线DD′的表达式为：y＝﹣x+7，

设点D′（n，7﹣n），

A，B，D为顶点的三角形与△ABC全等，

则BD′＝BC＝，

∴n=3或n=1

又∵AD′＝AC＝

∴n=3或n=7

∴n＝3，

故点D′（3，4）；

综上所述，符合条件的点D的坐标是：（4，3）或（3，4）．