题目内容
【题目】在“学本课堂”的实践中,王老师经常让学生以“问题”为中心进行自主、合作、探究学习.

(课堂提问)王老师在课堂中提出这样的问题:如图1,在Rt△ABC中,∠ACB=90°,∠BAC=30°,那么BC和AB有怎样的数量关系?
(互动生成)经小组合作交流后,各小组派代表发言.
(1)小华代表第3小组发言:AB=2BC. 请你补全小华的证明过程.
证明:把△ABC沿着AC翻折,得到△ADC.
∴∠ACD=∠ACB=90°,
∴∠BCD=∠ACD+∠ACB=90°+90°=180°,
即:点B、C、D共线.
(请在下面补全小华的证明过程)
(2)受到第3小组“翻折”的启发,小明代表第2小组发言:如图2,在△ABC中,如果把条件“∠ACB=90°”改为“∠ACB=135°”,保持“∠BAC=30°”不变,若BC=1,求AB的长.

(能力迁移)我们发现,翻折可以探索图形性质,请利用翻折解决下面问题.
如图3,点D是△ABC内一点,AD=AC,∠BAD=∠CAD=20°,∠ADB+∠ACB=210°,则AD、DB、BC三者之间的数量关系是 .

(课后拓展)如图4,在四边形ABCD中,∠BCD=45°,∠BAD=90°,∠ADB=∠CDB=60°,且AC=1,
则△ABD的周长为 .

【答案】(1)见解析;(2)![]() ;能力迁移:
;能力迁移:![]() ;课后拓展:
;课后拓展:![]() .
.
【解析】
(1)根据提示证明出△ABD为等边三角形即可说明BC和AB的关系;
(2)过点B作AC边的垂线,交AC的延长线于点D,设BD=x,则CD=BC=x,解出x即可;
能力迁移:把△ABD延AB边翻折得到△AEB,连接ED,EC,先通过角度转换得到∠EBC=90°,在证明BC=BD,EC=AD,即可求出AD、DB、BC三边的关系;
课后拓展:作BD⊥CD于点E,作CF垂直AD的延长线于点F,设AD=x,BD=2AD=2x,然后表示出AF,CF边建立方程解出x即可.
(1)证明:把△ABC沿着AC翻折,得到△ADC.
∴∠ACD=∠ACB=90°,
∴∠BCD=∠ACD+∠ACB=90°+90°=180°,
即:点B、C、D共线,
∴AB=AD,
∵∠BAC=30°,
∴∠ABC=60°,
∴△ABD为等边三角形,
∴AB=BD=2BC;
(2)过点B作AC边的垂线,交AC的延长线于点D,
∵∠ACB=135°,
∴∠BCD=45°,
∵∠BDC=90°,BC=1,
设BD=x,则CD=BC=x,
∴![]() ,解得:
,解得:![]() ,
,
∵∠BAC=30°,
∴AB=2BD=![]() ;
;

能力迁移:
把△ABD延AB边翻折得到△AEB,连接ED,EC,
∵∠BAD=∠CAD=20°,
∴∠EAB=20°,
∴∠EAC=60°,
∵∠ACB+∠ADB=210°,∠AEB=∠ADB,
∴∠ACB=∠AEB=210°,
∴∠EBC=360°-210°-60°=90°,
∵AD=AC,AE=AD,
∴AE=AC,
∴△AEC为等边三角形,
∴EC=AE=AD,
在Rt△EBC中,![]() ,
,
∵BC=BD,EC=AD,
∴![]() ;
;

课后拓展:
作BD⊥CD于点E,作CF垂直AD的延长线于点F,
∵∠BAD=90°,∠ADB=∠CDB=60°,
∴△BAD≌△BED,
∵∠BCD=45°,
∴BE=CE,
设AD=x,
∴BD=2AD=2x,
∴![]() ,
,
∴EC=EB=AB=![]() ,
,
∴DC=![]() ,
,
∴∠FDC=60°,∠ECD=30°,
∴DF=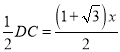 ,
,
∴ ,
,
 ,
,
∵AC=1,
在Rt△AFC中,![]() ,
,
则 ,解得:
,解得:![]() ,
,
AD=![]() ,
,
DB=![]() ,
,
则△ABD的周长为:![]() .
.


【题目】两家超市同时采取通过摇奖返现金搞促销活动,凡在超市购物满100元的顾客均可以参加摇奖一次.小明和小华对两家超市摇奖的50名顾客获奖情况进行了统计并制成了图表(如图)
奖金金额 获奖人数 | 20元 | 15元 | 10元 | 5元 |
商家甲超市 | 5 | 10 | 15 | 20 |
乙超市 | 2 | 3 | 20 | 25 |
(1)在甲超市摇奖的顾客获得奖金金额的中位数是 ,在乙超市摇奖的顾客获得奖金金额的众数是 ;
(2)请你补全统计图1;
(3)请你分别求出在甲、乙两超市参加摇奖的50名顾客平均获奖多少元?
(4)图2是甲超市的摇奖转盘,黄区20元、红区15元、蓝区10元、白区5元,如果你购物消费了100元后,参加一次摇奖,那么你获得奖金10元的概率是多少?







