题目内容
如图,已知半径为18cm的圆形纸片,如果要在这张纸片上裁剪出一个扇形作为圆锥的侧面,一个圆作为圆锥的底面,试问该如何裁剪,能使圆锥的底面圆面积尽量大,并且扇形的弧长恰好与圆锥底面圆的周长相配套(即两者长度相等),求出这时圆锥的表面积.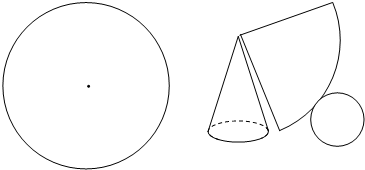
分析:根据题意可得出这个圆形纸板的半径等于小圆形的直径,设圆锥的半径为r,则这个圆形纸板的半径为2r,根据勾股定理得出圆锥的高为
r,从而得出这个圆形纸板的半径.
| 3 |
解答: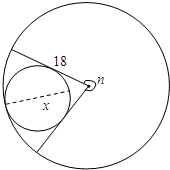
 解:若扇形的弧长与底面圆的周长长度相等,
解:若扇形的弧长与底面圆的周长长度相等,
则πx=
,即n=10x(0<x≤18),
∵n随着x的增大而增大,且当x=18时,
n=10×18=180,
即当底面小圆的直径恰好等于大圆的半径18cm时,
小圆与大圆的直径相切,扇形的弧长恰好与小圆的周长相配套,
此时圆锥的表面积为:S=π×(
)2+
×π×182=243π(cm2).

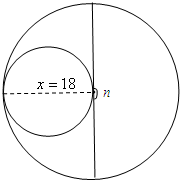
 解:若扇形的弧长与底面圆的周长长度相等,
解:若扇形的弧长与底面圆的周长长度相等,则πx=
| nπ×18 |
| 180 |
∵n随着x的增大而增大,且当x=18时,
n=10×18=180,
即当底面小圆的直径恰好等于大圆的半径18cm时,
小圆与大圆的直径相切,扇形的弧长恰好与小圆的周长相配套,
此时圆锥的表面积为:S=π×(
| 18 |
| 2 |
| 1 |
| 2 |
点评:本题考查了圆锥的计算,解决本题的关键是理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
相关题目
 ,并且每两个小圆的公共部分的面积都小于
,并且每两个小圆的公共部分的面积都小于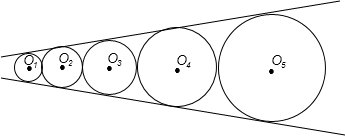
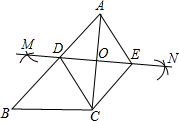 (2012•河源)如图,已知△ABC,按如下步骤作图:
(2012•河源)如图,已知△ABC,按如下步骤作图: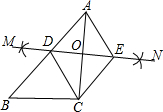 (2013•宛城区一模)如图,已知△ABC,按如下步骤作图:
(2013•宛城区一模)如图,已知△ABC,按如下步骤作图: