题目内容
(1)如图①,已知弧AB,用尺规作图,作出弧AB的圆心P;
(2)如图②,若弧AB半径PA为18,圆心角为120°,半径为2的⊙O,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙O自转多少周?

(2)如图②,若弧AB半径PA为18,圆心角为120°,半径为2的⊙O,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙O自转多少周?

分析:(1)连接AB,任意作一弦AC,然后分别作弦AB、AC的垂直平分线,相交于一点,则这点即为所求作的弧AB的圆心P;
(2)根据弧长计算公式求出弧AB的长度,然后求出⊙O在弧AB上滚动的周数,再根据⊙O在点B、A处分别旋转180°,正好自转1周,然后解答即可.
(2)根据弧长计算公式求出弧AB的长度,然后求出⊙O在弧AB上滚动的周数,再根据⊙O在点B、A处分别旋转180°,正好自转1周,然后解答即可.
解答: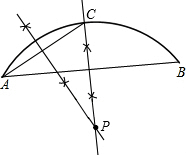 解:(1)如图所示,点P即为所求作的弧AB的圆心;
解:(1)如图所示,点P即为所求作的弧AB的圆心;
(2)弧AB的长=
=12π,
⊙O的周长=2πr=2π×2=4π,
∴⊙O滚动的长度为2×12π=24π,
滚动过程中自转周数=24π÷4π=6,
又⊙O在点B处由外侧转到内侧自转180°,在点A处由内侧转到外侧自转180°,正好等于1周,
6+1=7,
所以最后转回到初始位置,⊙O自转7周.
 解:(1)如图所示,点P即为所求作的弧AB的圆心;
解:(1)如图所示,点P即为所求作的弧AB的圆心;(2)弧AB的长=
| 120•π•18 |
| 180 |
⊙O的周长=2πr=2π×2=4π,
∴⊙O滚动的长度为2×12π=24π,
滚动过程中自转周数=24π÷4π=6,
又⊙O在点B处由外侧转到内侧自转180°,在点A处由内侧转到外侧自转180°,正好等于1周,
6+1=7,
所以最后转回到初始位置,⊙O自转7周.
点评:本题考查了弧的圆心的作法,根据垂径定理,作弧上的任意两弦的垂直平分线,交点即为所求作的圆心.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目


 ,O)、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,
,O)、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,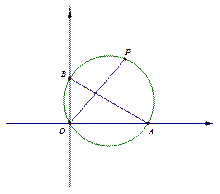
 ;
;

 ,O)、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,
,O)、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,
 ;
;
