题目内容
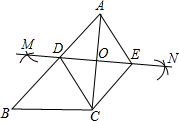 (2012•河源)如图,已知△ABC,按如下步骤作图:
(2012•河源)如图,已知△ABC,按如下步骤作图:①分别以A、C为圆心,以大于
| 1 | 2 |
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
(1)求证:四边形ADCE是菱形;
(2)当∠ACB=90°,BC=6,△ADC的周长为18时,求四边形ADCE的面积.
分析:(1)利用直线DE是线段AC的垂直平分线,得出AC⊥DE,即∠AOD=∠COE=90°,进而得出△AOD≌△COE,即可得出四边形ADCE是菱形;
(2)利用当∠ACB=90°时,OD∥BC,即有△ADO∽△ABC,即可得出AC和DE的长即可得出四边形ADCE的面积.
(2)利用当∠ACB=90°时,OD∥BC,即有△ADO∽△ABC,即可得出AC和DE的长即可得出四边形ADCE的面积.
解答: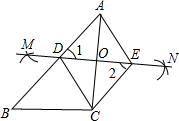 (1)证明:由题意可知:
(1)证明:由题意可知:
∵分别以A、C为圆心,以大于
AC的长为半径在AC两边作弧,交于两点M、N;
∴直线DE是线段AC的垂直平分线,
∴AC⊥DE,即∠AOD=∠COE=90°;
且AD=CD、AO=CO,
又∵CE∥AB,
∴∠1=∠2,
在△AOD和△COE中
,
∴△AOD≌△COE,
∴OD=OE,
∵A0=CO,DO=EO,
∴四边形ADCE是平行四边形,
又∵AC⊥DE,
∴四边形ADCE是菱形;
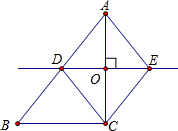
(2)解:当∠ACB=90°时,
OD∥BC,
即有△ADO∽△ABC,
 ∴
∴
=
=
,
又∵BC=6,
∴OD=3,
又∵△ADC的周长为18,
∴AD+AO=9,
即AD=9-AO,
∴OD=
=3,
可得AO=4,
∴DE=6,AC=8,
∴S=
AC•DE=
×8×6=24.
 (1)证明:由题意可知:
(1)证明:由题意可知:∵分别以A、C为圆心,以大于
| 1 |
| 2 |
∴直线DE是线段AC的垂直平分线,
∴AC⊥DE,即∠AOD=∠COE=90°;
且AD=CD、AO=CO,
又∵CE∥AB,
∴∠1=∠2,
在△AOD和△COE中
|
∴△AOD≌△COE,
∴OD=OE,
∵A0=CO,DO=EO,
∴四边形ADCE是平行四边形,
又∵AC⊥DE,
∴四边形ADCE是菱形;
(2)解:当∠ACB=90°时,
OD∥BC,
即有△ADO∽△ABC,
 ∴
∴| OD |
| BC |
| AO |
| AC |
| 1 |
| 2 |
又∵BC=6,
∴OD=3,
又∵△ADC的周长为18,
∴AD+AO=9,
即AD=9-AO,
∴OD=
| AD2-AO2 |
可得AO=4,
∴DE=6,AC=8,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了菱形的判定以及对角线垂直的四边形面积求法,根据已知得出△ADO∽△ABC进而求出AO的长是解题关键.

练习册系列答案
相关题目
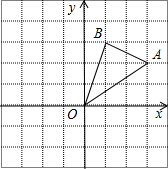 (2012•河源)如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.(直接填写答案)
(2012•河源)如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.(直接填写答案) (2012•河源)如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.①第一次到达G点时移动了
(2012•河源)如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.①第一次到达G点时移动了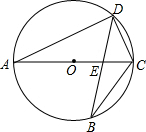 (2012•河源)如图,AC是⊙O的直径,弦BD交AC于点E.
(2012•河源)如图,AC是⊙O的直径,弦BD交AC于点E.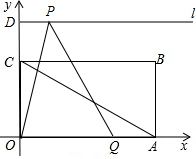 平行,点P、Q分别是l和x轴的正半轴上的动点,满足∠PQO=60°.
平行,点P、Q分别是l和x轴的正半轴上的动点,满足∠PQO=60°.