题目内容
如图,已知AB=AC+BD,∠CAB=∠ABD=90°AD交BC于P,⊙P与AB相切于点Q.设AC=a,BD=b(a≤b).(1)求⊙P的半径r;
(2)以AB为直径在AB的上方作半圆O(用尺规作图,保留痕迹,不写作法),请你探索⊙O与⊙P的位置关系,做出判断并加以证明;
(3)设a=2,b=4,能否在半圆O中,再画出两个与⊙P同样大小的⊙M和⊙N,使这3个小圆两两相交
 ,并且每两个小圆的公共部分的面积都小于
,并且每两个小圆的公共部分的面积都小于| 5 | .18 |
分析:(1)易证得△BPQ∽△BCA,△APQ∽△ADB,得到
=
,
=
,故可求得r的值;
(2)作出AB的中垂线交于AB于点O,以点O为圆心,AO为半径作半圆,即可,由于⊙O的半径R=
,⊙P的半径为r=
,可得到AQ=
=
=a,OQ=
-a=
,连接PO,由勾股定理得到PO=R-r,故⊙O与⊙P相切;
(3)用反证法判断.
| r |
| a |
| BQ |
| AB |
| r |
| b |
| AQ |
| AB |
(2)作出AB的中垂线交于AB于点O,以点O为圆心,AO为半径作半圆,即可,由于⊙O的半径R=
| a+b |
| 2 |
| ab |
| a+b |
| r•AB |
| b |
| 2Rr |
| b |
| a+b |
| 2 |
| b-a |
| 2 |
(3)用反证法判断.
解答: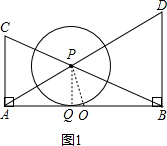 解:(1)如图1,连接PQ,
解:(1)如图1,连接PQ,
∵⊙P与AB相切于Q
∴PQ⊥AB且PQ=r
∵∠CAB=∠ABD=90°
∴△BPQ∽△BCA,△APQ∽△ADB
∴
=
,
=
∴
=
∴r=
;
(2)如图2:⊙O与⊙P相切,
证明:∵⊙O的半径R=
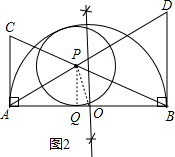
∴Rr=
∴AQ=
=
=a
OQ=
-a=
连接PO
则PO=
=
=
-
=R-r
∴⊙O与⊙P相切;
(3)由(2)知,半圆O的半径=
=3,
假设符合要求的图形存在,每两个圆的公共部分的面积分别为SPM、SMN、SPN,则它们均小于
π,又设每个小圆的面积为S,三个小圆公共部分的面积为SPMN,则三个小圆的覆盖面积=3S-(SPM+SMN+SPN)+SPMN>3π•(
)2-
π+SPMN≥
π=
π=半圆O的面积,而这是不可能的,故不能在这个半圆O中画出符合要求的⊙M和⊙N.
 解:(1)如图1,连接PQ,
解:(1)如图1,连接PQ,∵⊙P与AB相切于Q
∴PQ⊥AB且PQ=r
∵∠CAB=∠ABD=90°
∴△BPQ∽△BCA,△APQ∽△ADB
∴
| r |
| a |
| BQ |
| AB |
| r |
| b |
| AQ |
| AB |
∴
| a-r |
| a |
| r |
| b |
∴r=
| ab |
| a+b |
(2)如图2:⊙O与⊙P相切,
证明:∵⊙O的半径R=
| a+b |
| 2 |

∴Rr=
| ab |
| 2 |
∴AQ=
| r•AB |
| b |
| 2Rr |
| b |
OQ=
| a+b |
| 2 |
| b-a |
| 2 |
连接PO
则PO=
(
|
| a2+b2 |
| 2(a+b) |
| a+b |
| 2 |
| ab |
| a+b |
∴⊙O与⊙P相切;
(3)由(2)知,半圆O的半径=
| AB |
| 2 |
假设符合要求的图形存在,每两个圆的公共部分的面积分别为SPM、SMN、SPN,则它们均小于
| 5 |
| 18 |
| 4 |
| 3 |
| 3×5 |
| 18 |
| 9 |
| 2 |
| 32 |
| 2 |
点评:本题利用了相似三角形的判定和性质,勾股定理,圆的面积公式,反证法求解,还考查了圆的作法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,则∠BFD的度数是( )
如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,则∠BFD的度数是( )| A、60° | B、90° | C、45° | D、120° |
 10、如图,已知AB=AC,D是BC的中点,E是AD上的一点,图中全等三角形有几对( )
10、如图,已知AB=AC,D是BC的中点,E是AD上的一点,图中全等三角形有几对( ) 26、如图,已知AB=AC,AD=AE.求证BD=CE.
26、如图,已知AB=AC,AD=AE.求证BD=CE. 2、如图,已知AB=AC,AD=AE,BD=EC,则图中有
2、如图,已知AB=AC,AD=AE,BD=EC,则图中有 如图,已知AB=AC,BC=CD=AD,求∠B的值.
如图,已知AB=AC,BC=CD=AD,求∠B的值.