题目内容
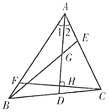
【题目】如图所示,在△ABC中,∠1=∠2,点G为AD的中点,连接BG并延长,交AC于点E,F为AB上一点,且CF⊥AD于点H,下列判断中:①AD是△ABE的角平分线;②BE是△ABD边AD上的中线;③CH是△ACD边AD上的高.正确的个数有( )
A. 0个B. 1个C. 2个D. 3个
【答案】B
【解析】
对于①,根据角平分线的定义和已知可以判断AG是△ABE的角平分线,据此判断①是否正确;
对于②,根据已知可以判断BG是△ABD边AD上的中线,据此可对②进行判断;
对于③,根据CF⊥AD于H,结合三角形的高的定义即可判断③.
∵∠1=∠2,
∴AG是△ABE的角平分线,
∴AD不是△ABE的角平分线.故①错误.
∵G为△ABD边AD的中点,
∴BG是△ABD边AD上的中线,
∴BE不是△ABD边AD上的中线.故②错误.
∵CF⊥AD于H,
∴CH为△ACD的边AD上的高.故③正确.
综上可知,正确的结论只有1个.
故选B.

练习册系列答案
相关题目
【题目】目前节能灯在城市已基本普及,为满足消费者需求,某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价、标价如下表:
进价(元/只) | 标价(元/只) | |
甲型 | 25 | 40 |
乙型 | 45 | 60 |
(1)如何进货才能保证进货款恰好为46000元?
(2)由于恰逢五一,商场决定搞促销活动,乙型节能灯打八五折,请你运用所学的知识预算一下甲型节能灯要打几折才能使这批灯售完后获得9200元的利润(不考虑其它因素)?