题目内容
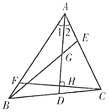
【题目】把一个等腰直角三角板放在黑板上画好了的平面直角坐标系内,如图,已知直角顶点A的坐标为(0,1),另一个顶点B的坐标为(﹣5,5),则点C的坐标为________.
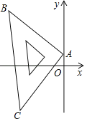
【答案】(﹣4,﹣4)
【解析】
如图,过点B、C分别作BG⊥y轴、CH⊥y轴,先根据AAS证明△ABG≌△CAH,从而可得AG=CH,BG=AH,再根据A、B两点的坐标即可求出OH、CH的长,继而可得点C的坐标.
解:过点B、C分别作BG⊥y轴、CH⊥y轴,垂足分别为G、H,则∠AGB=∠CHA=90°,∠ABG+∠BAG=90°,
∵∠BAC=90°,∴∠CAH+∠BAG=90°,∴∠ABG=∠CAH,
又∵AB=AC,∴△ABG≌△CAH(AAS).
∴AG=CH,BG=AH,
∵A(0,1),∴OA=1,∵B(﹣5,5),∴BG=5,OG=5,
∴AH=5,AG=OG-OA=5-1=4,
∴CH=4,OH=AH-OA=5-1=4,
∴点C的坐标为(―4,―4).
故答案为(―4,―4).


练习册系列答案
相关题目
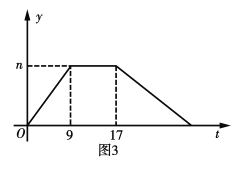
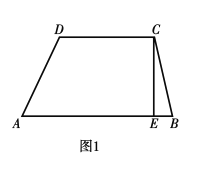
【题目】如图1,梯形![]() 中,上底
中,上底![]() 下底
下底![]() 高
高![]() 梯形的面积
梯形的面积![]() 动点
动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向,以每秒
方向,以每秒![]() 个单位长度的速度匀速运动.
个单位长度的速度匀速运动.
![]() 请根据
请根据![]() 与
与![]() 的关系式,完成下列问题:
的关系式,完成下列问题:
|
|
|
|
| ··· | |
|
|
|
| ··· |
![]() 补充表格中的数据;
补充表格中的数据;
![]() 当
当![]() 时,表示的图形是_ .
时,表示的图形是_ .
![]() 梯形的面积
梯形的面积![]() 与
与![]() 的关系如图2所示,则点
的关系如图2所示,则点![]() 表示的实际意义是_ ;
表示的实际意义是_ ;

![]() 若点
若点![]() 运动的时间为
运动的时间为![]() 的面积为
的面积为![]() 与
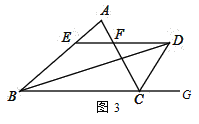
与![]() 的关系如图3所示.求
的关系如图3所示.求![]() 的长和
的长和![]() 的值.
的值.