题目内容
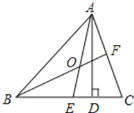
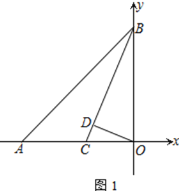
【题目】如图,A(-t,0)、B(0,t),其中t>0,点C为OA上一点,OD⊥BC于点D,且∠BCO=45°+∠COD
(1) 求证:BC平分∠ABO
(2) 求![]() 的值
的值
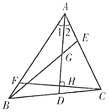
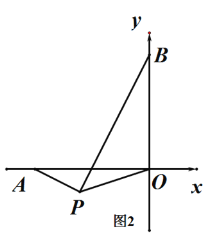
(3) 若点P为第三象限内一动点,且∠APO=135°,试问AP和BP是否存在某种确定的位置关系?说明理由
【答案】(1)见解析;(2)2;(3)BP⊥AP,理由见解析;
【解析】
(1)分别证明:∠ABC=∠DOC,∠CBO=∠DOC即可.
(2)在BC上截DE=DO,证CE=OE=BE,则E为BC的中点,则BC=2EC=2(DE+DC)=2(OD+CD),代入化简即可,也可以用四点共圆去思考更加简单.
(3)作OM⊥OP交PB于M,交AP的延长线于N,在证明△BOP≌△AON,即可解答.
(1)证明:如图1中,∵AO=BO=t,∠AOB=90°,
∴∠OAB=∠OBA=45°,
∵∠BCO=45°+∠COD=∠BAO+∠ABC,
∴∠COD=∠ABC,
∵OD⊥BC,
∴∠CDO=90°,
∵∠DOC+∠DCO=90°,∠CBO+∠BCO=90°,
∴∠DOC=∠CBO,
∴∠ABC=∠CBO.
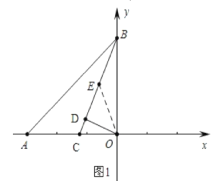
(2)中图1中,作DE=DO,
∵∠ODE=90°,
∴∠DEO=45°=∠EBO+∠EOB,
∵∠ABC=∠CBO=![]() ∠ABO=22.5°,
∠ABO=22.5°,
∴∠EOB=∠EBO=22.5°,
∴EB=EO,
∵∠ECO=∠EOC=67.5°,
∴EC=EO,
∴BC=2EC=2(DE+CD)=2OD+2CD,
∴![]() =2.
=2.
(3)结论:BP⊥AP,如图2,理由如下:
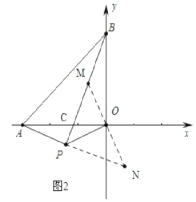
作OM⊥OP交PB于M,交AP的延长线于N,
∵∠APO=135°,
∴∠OPN=∠N=45°,
∴OP=ON,
∵∠AOB=∠PON=90°,
∴∠BOP=∠AON,
在△OBP和△OAN中,
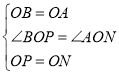 ,
,
∴△BOP≌△AON,
∴∠BPO=∠N=45°,
∵∠OPN=45°,
∴∠BPN=∠BPO+∠OPN=90°,
∴BP⊥AP.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案