题目内容
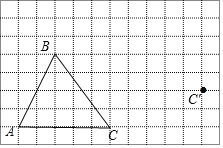
【题目】如图， 在平面直角坐标系xOy中，三角形ABC三个顶点的坐标分别为（-2，-2），（3,1），（0,2），若把三角形ABC向上平移 3 个单位长度，再向左平移 
个单位长度得到三角形 
，点A，B，C的对应点分别为 
，
，
.
（1）写出点 ，， 的坐标；
（2）在图中画出平移后的三角形 ；
（3）三角形 的面积为__________．
【答案】（1）点A′的坐标为（-3，01）、点B′的坐标为（2，4），点C′的坐标为（-1，5）；（2）作图见解析；（3）7.
【解析】（1）根据“横坐标，右移加，左移减；纵坐标，上移加，下移减”即可得；
（2）顺次连接
，
，
即可得三角形
；
（3）利用割补法，用长方形的面积减去外三个三角形的面积可得．
（1）∵点A的坐标为（-2，-2）、点B的坐标为（3，1），点C的坐标为（0，2），
∴向上平移3个单位长度，再向左平移1个单位长度后点的坐标为（-3，01）、点的坐标为（2，4），点的坐标为（-1，5）；
（2）平移后的图形如图所示.
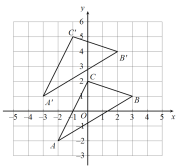
（3）三角形的面积=5×4
7.
阅读快车系列答案【题目】学完二次根式一章后，小易同学看到这样一题：“函数
中,自变量
的取值范围是什么？”这个问题很简单，根据二次根式的性质很容易得到自变量的取值范围.联想到一次函数，小易想进一步研究这个函数的图象和性质.以下是他的研究步骤：
第一步：函数中,自变量的取值范围是_____________.
第二步：根据自变量取值范围列表：
| -1 | 0 | 1 | 2 | 3 | 4 | |
| 0 | 1 |
|
| 2 |
|
__________.
第三步：描点画出函数图象.
在描点的时候，遇到了
，
这样的点，小易同学用所学勾股定理的知识，找到了画图方法，如图所示：
你能否从中得到启发，在下面的
轴上标出表示
、
、
的点，并画出的函数图象.
第四步：分析函数的性质.
请写出你发现的函数的性质(至少写两条)：
____________________________________________________________________________________________
____________________________________________________________________________________________
第五步：利用函数图象解含二次根式的方程和不等式.
（1）请在上面坐标系中画出
的图象，并估算方程
的解.
（2）不等式
的解是__________________.
