题目内容
【题目】如图,在△ABC中,∠B=90°,AB=8厘米,BC=6厘米,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动速度为1厘米/秒,点Q从点B开始沿B→C→A方向运动速度为2厘米/秒,若它们同时出发,设出发的时间为t秒.
(1)求出发2秒后,PQ的长;
(2)点Q在CA边上运动时,当△BCQ成为等腰三角形时,求点Q的运动时间.
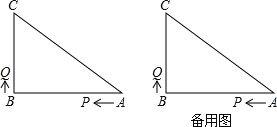
【答案】(1)![]() 厘米;(2)当t为5.5秒或6秒或6.6秒时,△BCQ为等腰三角形.
厘米;(2)当t为5.5秒或6秒或6.6秒时,△BCQ为等腰三角形.
【解析】
(1)运动2秒后,根据P、Q运动速度可知道运动的路程BQ和AP长,在Rt△QBP中,利用勾股定理即可求出PQ.
(2)已知点Q在CA边上运动时,若△BCQ成为等腰三角形,可分三种情况讨论,即CQ=BQ,CQ=BC,BC=BQ,得出点Q运动的路程,已知速度即可求出运动时间,在直角三角形中可利用勾股定理求解.
(1)BQ=2×2=4cm,
BP=AB﹣AP=8﹣2×1=6cm.
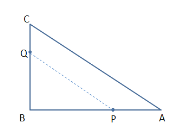
∵∠B=90°,
PQ=![]() (cm);
(cm);
故答案为:![]() 厘米
厘米
(2)分三种情况:
①当CQ=BQ时,如图1所示:
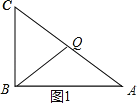
则∠C=∠CBQ.
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°,
∵∠A+∠C=90°,
∴∠A=∠ABQ
∴BQ=AQ,
∴BQ是Rt△ABC斜边上的中线
∵AC=![]()
∴CQ=AQ=5,
∴BC+CQ=11,
∴t=11÷2=5.5秒.
②当CQ=BC时,如图2所示:
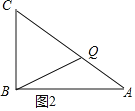
则BC+CQ=12
∴t=12÷2=6秒.
③当BC=BQ时,如图3所示:
过B点作BE⊥AC于点E,
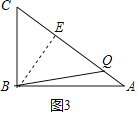
则BE![]() (cm)
(cm)
∴CE=![]() cm,
cm,
∴CQ=2CE=7.2cm,
∴BC+CQ=13.2cm,
∴t=13.2÷2=6.6秒.
综上所述,当t为5.5秒或6秒或6.6秒时,
△BCQ为等腰三角形.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目