题目内容
【题目】如图,四边形ABCD是正方形,△ADF按顺时针方向旋转一定角度后得到△ABE,
若AF=4,AB=7.
(1)旋转中心为______;旋转角度为______;
(2)DE的长度为______;
(3)指出BE与DF的位置关系如何?并说明理由.
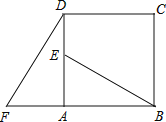
【答案】(1)A,90°;(2)3;(3)BE⊥DF,理由见解析.
【解析】(1)(2)利用旋转的定义和性质即可得出答案;(3)利用旋转证出△ABE≌△ADF,再通过全等三角形的性质、三角形内角和即可证出.
解:(1)旋转中心为点A,旋转角度为90°;
(2)DE=AD-AE=7-4=3;
(3)BE⊥DF.理由如下:
延长BE与DF交于点M
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴∠ABE=∠ADF,
∵∠ADF+∠F=180°-90°=90°,
∴∠ABE+∠F=90°,
即∠BMF=90°,∴BE⊥DF.

练习册系列答案
相关题目
【题目】某校篮球队13名同学的身高如下表:
身高(cm) | 175 | 180 | 182 | 185 | 188 |
人数(个) | 1 | 5 | 4 | 2 | 1 |
则该校篮球队13名同学身高的众数和中位数分别是( )
A.182,180
B.180,180
C.180,182
D.188,182